Tags:
Quelle: CI Teil 1 Lecture 2
Quelle: CI Teil 1 Lecture 2
Tags:
Quelle: CI Teil 1 Lecture 2
Quelle: CI Teil 1 Lecture 2
How many local minima may the cost function for linear regression have (under regular conditions)?
1
Tags:
Quelle: CI Teil 1 Lecture 2
Quelle: CI Teil 1 Lecture 2
Tags:
Quelle: CI Teil 1 Lecture 2
Quelle: CI Teil 1 Lecture 2
General gradient descent formula?
Für ein Feature:

Für mehrere Features:
h_theta(x) = x^T * theta

Für mehrere Features:
h_theta(x) = x^T * theta
Tags:
Quelle: CI Teil 1 Lecture 2
Quelle: CI Teil 1 Lecture 2
Tags:
Quelle: CI Teil 1 Lecture 2
Quelle: CI Teil 1 Lecture 2
What issues can arise during gradient descent?
- Kann in lokalem Minimum hängenbleiben
- Lernrate kann zu langsam sein -> Langsames Konvergieren
- Lernrate kann zu schnell sein -> Ergebnis divergiert und / oder oszilliert.
Tags:
Quelle: CI Teil 1 Lecture 2
Quelle: CI Teil 1 Lecture 2
What is the design matrix? What are its dimensions?
m....Anzahl an trainingsdatensätzen
n....Anzahl an Eigenschaften (Features)
Die designmatrix X besteht aus den Eigenschaften (Features) der trainingsdaten (wobei immer ein x_0 = 1 dazu gehört) untereinander angeordnet.
Sie hat die dimension m x (n+1). D.h. m Zeilen mit n+1 spalten (von x_0 bis x_n).
n....Anzahl an Eigenschaften (Features)
Die designmatrix X besteht aus den Eigenschaften (Features) der trainingsdaten (wobei immer ein x_0 = 1 dazu gehört) untereinander angeordnet.
Sie hat die dimension m x (n+1). D.h. m Zeilen mit n+1 spalten (von x_0 bis x_n).
Analytical solution for linear regression?
What are the components of the solution?
What are the components of the solution?
 = Ideale Parameter
= Ideale Parameter 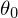 bis
bis 

Wichtigste Komponente
 ...Moore Penrose Pseudoinverse von
...Moore Penrose Pseudoinverse von 
 ...design matrix
...design matrix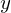 ...output vector
...output vectorTags:
Quelle: CI Teil 1 Lecture 2
Quelle: CI Teil 1 Lecture 2
Pros and Cons of gradiant descent vs. analytical solutions
Gradiant Descent:
Pros:
Cons:
Analytical Solution:
Pros:
Cons:
Pros:
- Funktioniert auch mit großer Anzahl an eingangs features
Cons:
- Lernrate
 muss gewählt werden
muss gewählt werden - Iterativer Algorithmus braucht viele iterationen um zu konvergieren.
Analytical Solution:
Pros:
- Lernrate
 muss nicht gewählt werden
muss nicht gewählt werden - Direkte Lösung (keine iterationen)
Cons:
- Langsam wenn
 zu groß ist (da eine nxn matrix invertiert werden muss).
zu groß ist (da eine nxn matrix invertiert werden muss).
Tags:
Quelle: CI Teil 1 Lecture 2
Quelle: CI Teil 1 Lecture 2
How can one learn non-linear hypotheses with linear regression?
Durch das einbinden der nicht-linearen eigenschaften in die Designmatrix 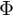 . (design matrix with non-linear features)
. (design matrix with non-linear features)
Die Hypothese behält die gleiche Form aber die Werte in der Designmatrix ändern sich.
z.b.

Es wird eine nichtlineare Basisfunktion angewendet.
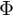 . (design matrix with non-linear features)
. (design matrix with non-linear features)Die Hypothese behält die gleiche Form aber die Werte in der Designmatrix ändern sich.
z.b.

Es wird eine nichtlineare Basisfunktion angewendet.
Tags:
Quelle: CI Teil 1 Lecture 2
Quelle: CI Teil 1 Lecture 2
What is polynomial regression?
Das ist eine nichtlineare Regression bei der die Eigenschaften (Features) potenzen von x sind.


Tags:
Quelle: CI Teil 1 Lecture 2
Quelle: CI Teil 1 Lecture 2
What are radial basis functions?
Das sind nichtlinear basisfunktionen bei denen Gaus'sche Glockenkurven verwendet wird.
Jede Basisfunktion hat einen Mittelpunkt im Eingangsraum.
im Eingangsraum.
Alle Basisfunktionen teilen sich ein sigma das die breite der Basisfunktion angibt.
das die breite der Basisfunktion angibt.

Jede Basisfunktion hat einen Mittelpunkt
 im Eingangsraum.
im Eingangsraum.Alle Basisfunktionen teilen sich ein sigma
 das die breite der Basisfunktion angibt.
das die breite der Basisfunktion angibt.
Tags:
Quelle: CI Teil 1 Lecture 2
Quelle: CI Teil 1 Lecture 2
Logistic regression is a method for ... ?
Logistic regression ist eine Methode für binäre Klassifikation.
Tags:
Quelle: CI Teil 1 Lecture 3
Quelle: CI Teil 1 Lecture 3
Logistic regression hypothesis?

Logistic regression benutzt eine sigmoide basisfunktion. Diese ist gegenüber der Sprungfunktion ableitbar (für gradiant descent notwendig) und besitzt zusätzliche information über die sicherheit der vorhersage.
Tags:
Quelle: CI Teil 1 Lecture 3
Quelle: CI Teil 1 Lecture 3
What's the cost function used for logistic regression?
Is this function convex or non-convex?
Is this function convex or non-convex?
 wenn y = 1 oder
wenn y = 1 oder  für y = 0
für y = 0Mittelwert über Kostenfunktion:

Diese Funktion ist convex (d.h. einzigartiges lokales / globales minimum).
Tags:
Quelle: CI Teil 1 Lecture 3
Quelle: CI Teil 1 Lecture 3
What does adaptive learning rate mean in the context of gradiant descent?
Bei einer adaptiven Lernrate wird die Lernrate leicht erhöht wenn sich der Wert der Kostenfunktion seit den letzten Parametern verringert hat.
Wenn der Wert der Kostenfunktion für die neuen Parameter höher ist als für die alten dann werden die neuen Parameter nicht übernommen und die Lernrate moderat verringert.
Wenn der Wert der Kostenfunktion für die neuen Parameter höher ist als für die alten dann werden die neuen Parameter nicht übernommen und die Lernrate moderat verringert.
Tags:
Quelle: CI Teil 1 Lecture 3
Quelle: CI Teil 1 Lecture 3
How to evaluate a hypothesis?
Um eine Hypothese zu bewerten werden die vorhandenen Datensätze in 2 Teile geteilt.
Ein Satz Trainingsdaten mit denen die Hypothese gebildet wird und ein Satz Testdaten (die nicht für die Hypothesenbildung verwendet werden) mit denen die Hypothese getestet wird.
Wenn die Hypothese zu stark an die Trainingsdaten angepasst ist (over-fitting) dann ist der fehler bei den Trainingsdaten zwar geringer aber der fehler bei den Testdaten hoch.
Wenn die Hypothese zu schwach an die Trainingsdaten angepasst ist (under-fitting) dann ist der fehler bei den Trainingsdaten und bei den Testdaten höher als er sein müsste.
Wenn die Hypothese genau richtig komplex ist dann ist der fehler bei Trainings und Testdaten minimal.
Ein Satz Trainingsdaten mit denen die Hypothese gebildet wird und ein Satz Testdaten (die nicht für die Hypothesenbildung verwendet werden) mit denen die Hypothese getestet wird.
Wenn die Hypothese zu stark an die Trainingsdaten angepasst ist (over-fitting) dann ist der fehler bei den Trainingsdaten zwar geringer aber der fehler bei den Testdaten hoch.
Wenn die Hypothese zu schwach an die Trainingsdaten angepasst ist (under-fitting) dann ist der fehler bei den Trainingsdaten und bei den Testdaten höher als er sein müsste.
Wenn die Hypothese genau richtig komplex ist dann ist der fehler bei Trainings und Testdaten minimal.
Tags:
Quelle: CI Teil 1 Lecture 3
Quelle: CI Teil 1 Lecture 3
What is under-/over-fitting?
Wenn die Hypothese zu stark an die Trainingsdaten angepasst ist (over-fitting) dann ist der fehler bei den Trainingsdaten zwar geringer aber der fehler bei den Testdaten hoch.
Wenn die Hypothese zu schwach an die Trainingsdaten angepasst ist (under-fitting) dann ist der fehler bei den Trainingsdaten und bei den Testdaten höher als er sein müsste.
Wenn die Hypothese genau richtig komplex ist dann ist der fehler bei Trainings und Testdaten minimal.
Wenn die Hypothese zu schwach an die Trainingsdaten angepasst ist (under-fitting) dann ist der fehler bei den Trainingsdaten und bei den Testdaten höher als er sein müsste.
Wenn die Hypothese genau richtig komplex ist dann ist der fehler bei Trainings und Testdaten minimal.
Tags:
Quelle: CI Teil 1 Lecture 3
Quelle: CI Teil 1 Lecture 3
What is model selection?
Hier ist die Idee das man noch abstraktere Parameter einführt (komplexität des models, art des Lernalgorithmuses) und die Daten in 3 Teile teilt.
Trainingsdaten, Validierungsdaten und Testdaten.
Aus den Trainingsdaten werden die Hypothesen gebildet (für verschiedene abstrake Parameter).
Über die Validierungsdaten wird jene Hypothese ausgewählt die den geringsten fehler bei den Validierungsdaten hat.
Über die Testdaten wird die performance der ausgewählten Hypothese abgeschätzt.
Trainingsdaten, Validierungsdaten und Testdaten.
Aus den Trainingsdaten werden die Hypothesen gebildet (für verschiedene abstrake Parameter).
Über die Validierungsdaten wird jene Hypothese ausgewählt die den geringsten fehler bei den Validierungsdaten hat.
Über die Testdaten wird die performance der ausgewählten Hypothese abgeschätzt.
Tags:
Quelle: CI Teil 1 Lecture 3
Quelle: CI Teil 1 Lecture 3
What are training, validation and test sets?
Hier ist die Idee das man noch abstraktere Parameter einführt (komplexität des models, art des Lernalgorithmuses) und die Daten in 3 Teile teilt um verschieden Modelle zu testen.
Trainingsdaten, Validierungsdaten und Testdaten.
Aus den Trainingsdaten werden die Hypothesen gebildet (für verschiedene abstrake Parameter).
Über die Validierungsdaten wird jene Hypothese ausgewählt die den geringsten fehler bei den Validierungsdaten hat.
Über die Testdaten wird die performance der ausgewählten Hypothese abgeschätzt.
Trainingsdaten, Validierungsdaten und Testdaten.
Aus den Trainingsdaten werden die Hypothesen gebildet (für verschiedene abstrake Parameter).
Über die Validierungsdaten wird jene Hypothese ausgewählt die den geringsten fehler bei den Validierungsdaten hat.
Über die Testdaten wird die performance der ausgewählten Hypothese abgeschätzt.
Tags:
Quelle: CI Teil 1 Lecture 3
Quelle: CI Teil 1 Lecture 3
How does model selection work? (Procedure)
Hier ist die Idee das man noch abstraktere Parameter einführt (komplexität des models, art des Lernalgorithmuses) und die Daten in 3 Teile teilt um verschieden Modelle zu testen.
Trainingsdaten, Validierungsdaten und Testdaten.
Aus den Trainingsdaten werden die Hypothesen gebildet (für verschiedene abstrake Parameter).
Über die Validierungsdaten wird jene Hypothese ausgewählt die den geringsten fehler bei den Validierungsdaten hat.
Über die Testdaten wird die performance der ausgewählten Hypothese abgeschätzt.
Verschiedene lernalgorithmen werden also mit dem selben Trainingset gefüttert.
Daraus entstehen verschiedene Hypothesen.
Über die Validierungsdaten wird jene Hypothese ausgewählt die den niedrigsten validation error (kosten) hat.
Über die unabhängigen Testdaten wird der testfehler / testkosten der ausgewählten Hypothese bestimmt.
Trainingsdaten, Validierungsdaten und Testdaten.
Aus den Trainingsdaten werden die Hypothesen gebildet (für verschiedene abstrake Parameter).
Über die Validierungsdaten wird jene Hypothese ausgewählt die den geringsten fehler bei den Validierungsdaten hat.
Über die Testdaten wird die performance der ausgewählten Hypothese abgeschätzt.
Verschiedene lernalgorithmen werden also mit dem selben Trainingset gefüttert.
Daraus entstehen verschiedene Hypothesen.
Über die Validierungsdaten wird jene Hypothese ausgewählt die den niedrigsten validation error (kosten) hat.
Über die unabhängigen Testdaten wird der testfehler / testkosten der ausgewählten Hypothese bestimmt.
Tags:
Quelle: CI Teil 1 Lecture 3
Quelle: CI Teil 1 Lecture 3
What types of neural networks are there?
Es gibt biologische neurale Netzwerke (gehirn) und künstliche neurale netzwerke (ANN).
Bei den ANNs unterscheide man noch zwischen:
Bei den ANNs unterscheide man noch zwischen:
- Feedforward Networks
- Self Organizing Maps
- Recurrent Networks
- Spiking Neural Network
Tags:
Quelle: CI Teil 1 Lecture 4
Quelle: CI Teil 1 Lecture 4
What are ANNs?
Artificial Neural Networks sind netzwerke aus Neuronen. Diese Neuronen erhalten gewichtete Eingangswerte und berechnen dann den Ausgang des Neurons über eine Aktivierungsfunktion (z.b. step-function, sigmoide Funktion etc...).
Tags:
Quelle: CI Teil 1 Lecture 4
Quelle: CI Teil 1 Lecture 4
Types of ANN?
- Feedforward Network
- SOM (Self Organizing Map)
- Recurrent Network
- Spiking Neural Network
Tags:
Quelle: CI Teil 1 Lecture 4
Quelle: CI Teil 1 Lecture 4
Applications of ANNs?
- Funktionsapproximierung / Regression
- Klassifikation
- Datenverarbeitung
- Robotik
Tags:
Quelle: CI Teil 1 Lecture 4
Quelle: CI Teil 1 Lecture 4
Artificial Neuron Model?
Ein künstliches Neuron besteht aus:
x....Input vektor (x0,...xn) (x0 = 1)
w...Weights (w0,...wn) (w0 = b)
b....bias / offset
f....Activation funktion
z...output
z = f(w^T*x)
x....Input vektor (x0,...xn) (x0 = 1)
w...Weights (w0,...wn) (w0 = b)
b....bias / offset
f....Activation funktion
z...output
z = f(w^T*x)
Tags:
Quelle: CI Teil 1 Lecture 4
Quelle: CI Teil 1 Lecture 4
What is an activation function?
Types and usages
Types and usages
Die Aktivierungsfunktion ist eine funktion die den Output (z) des Neurons basierend auf den gewichten (w) und dem eingang (x) berechnet.
Beispiele für Aktivierungsfunktionen sind:
Beispiele für Aktivierungsfunktionen sind:
- Step-function (für binäre Klassifikation)
- Lineare Funktion (für lineare Regression)
- Sigmoide-Funktion (für nichtlineare-regression und klassifikation)
Tags:
Quelle: CI Teil 1 Lecture 4
Quelle: CI Teil 1 Lecture 4
What is Perceptron?
Perceptron ist das einfachste neurale Netzwerk für die klassifikation linear trennbarer Daten. Es ist also ein linearer, binärer Klassifikator.
Perceptron besteht aus einem Neuron mit der Step-Funktion als Aktivierungsfunktion.
Perceptron besteht aus einem Neuron mit der Step-Funktion als Aktivierungsfunktion.
Tags:
Quelle: CI Teil 1 Lecture 4
Quelle: CI Teil 1 Lecture 4
Convergence properties of Perceptron?
Wenn die Trainingsdaten linear trennbar sind dann konvergiert der Algorithmus.
Wenn die Trainingsddaten nicht linear trennbar sind dann konvergiert der Algorithmus nicht.
Wenn die Trainingsddaten nicht linear trennbar sind dann konvergiert der Algorithmus nicht.
Tags:
Quelle: CI Teil 1 Lecture 4
Quelle: CI Teil 1 Lecture 4
Binary learning classification with Perceptron?
Wenn die Trainingsdaten linear Trennbar sind dann existieren gewichte w sodass
a = w^T*x^(i) < 0 für alle x^(i) in Klasse 0
a = w^T*x^(i) >= 0 für alle x^(i) in Klasse 1
f(a) = 0 für a < 0
f(a) = 1 für a >= 0
Wenn das Sample richtig klassifiziert wurde ändern sich die Gewichte nicht.
Wenn das Sample falsch klassifiziert wurde ändern sich die gewichte folgendermaßen:
w := w + eta*(y^(i)-z)x^(i)
a = w^T*x^(i) < 0 für alle x^(i) in Klasse 0
a = w^T*x^(i) >= 0 für alle x^(i) in Klasse 1
f(a) = 0 für a < 0
f(a) = 1 für a >= 0
Wenn das Sample richtig klassifiziert wurde ändern sich die Gewichte nicht.
Wenn das Sample falsch klassifiziert wurde ändern sich die gewichte folgendermaßen:
w := w + eta*(y^(i)-z)x^(i)
Tags:
Quelle: CI Teil 1 Lecture 4
Quelle: CI Teil 1 Lecture 4
Learning algorithm of Perceptron?
Für jedes Sample x^(i) der Trainingsdaten:
keine Änderung der Gewichte wenn das Sample richtig klassifiziert wurde (also z = 0 für y^(i) = 0 und z = 1 für y^(i) = 1).
Wenn das Sample falsch klassifiziert wurde ändern sich die gewichte folgendermaßen:
w := w + eta*(y^(i)-z)x^(i)
keine Änderung der Gewichte wenn das Sample richtig klassifiziert wurde (also z = 0 für y^(i) = 0 und z = 1 für y^(i) = 1).
Wenn das Sample falsch klassifiziert wurde ändern sich die gewichte folgendermaßen:
w := w + eta*(y^(i)-z)x^(i)
Tags:
Quelle: CI Teil 1 Lecture 4
Quelle: CI Teil 1 Lecture 4
Limitations of Perceptron?
Wenn die Daten nicht linear trennbar sind dann kann kein linearer Klassifikator alle Daten richtig klassifizieren (also auch Perceptron nicht).
Bei Perceptron konvergiert der algorithmus nicht wenn die daten nicht linear trennbar sind.
Bei Perceptron konvergiert der algorithmus nicht wenn die daten nicht linear trennbar sind.
Tags:
Quelle: CI Teil 1 Lecture 4
Quelle: CI Teil 1 Lecture 4
Can you use Perceptron to classify nonlinear data?
Ja aber nur wenn man Perceptron erweitert (Kernel Perceptron). Normalerweise kann Perceptron nichtlineare Daten nicht korrekt klassifizieren.
Tags:
Quelle: CI Teil 1 Lecture 4
Quelle: CI Teil 1 Lecture 4
What is feed forward architecture?
Bei feed forward architektur besteht das Netzwerk auf verschiedenen Knoten (Neuronen) die miteinander verbunden sind.
In diesem Netzwerk gibt es keine Kreise oder Rückwärtsbewegung.
Die Inputinformation wird von den Inputneuronen zu den Outputneuronen ausgebreitet.
In diesem Netzwerk gibt es keine Kreise oder Rückwärtsbewegung.
Die Inputinformation wird von den Inputneuronen zu den Outputneuronen ausgebreitet.
Tags:
Quelle: CI Teil 1 Lecture 4
Quelle: CI Teil 1 Lecture 4
What is the hidden layer and what is it useful for?
Das Hidden Layer ist eine (oder mehrere) Ebenen von Neuronen zwischen Input und Output Neuronen.
Diese haben die gewichteten Ausgänge der vorhergehenden Neuronen als Eingang.
Damit ist es möglich nichtlineare Funktionen und die kombination von Inputvariablen abzudecken.
Diese haben die gewichteten Ausgänge der vorhergehenden Neuronen als Eingang.
Damit ist es möglich nichtlineare Funktionen und die kombination von Inputvariablen abzudecken.
Tags:
Quelle: CI Teil 1 Lecture 4
Quelle: CI Teil 1 Lecture 4
What function implements ANN with 1 hidden layer with sigmoid activation function?
Wenn die Output Neuronen eine sigmoide aktivierungsfunktion haben dann implementiert das ANN eine Klassifikation.
Wenn die Output Neuronen eine lineare Aktivierungsfunktion haben dann implementiert das ANN die Regression.
Wenn die Output Neuronen eine lineare Aktivierungsfunktion haben dann implementiert das ANN die Regression.
Tags:
Quelle: CI Teil 1 Lecture 4
Quelle: CI Teil 1 Lecture 4
Can Perceptron solve XOR?
How about Multilayer Perceptron?
How about Multilayer Perceptron?
Perceptron kann XOR nicht lösen (nicht linear trennbar).
MLP kann XOR lösen.
MLP kann XOR lösen.
Tags:
Quelle: CI Teil 1 Lecture 4
Quelle: CI Teil 1 Lecture 4
Computational properties of ANN?
Jede Bool'sche Funktion kann mit einem Hidden Layer abgebildet werden (benötigt aber eventuel exponentielle Anzahl an Hidden Neurons).
Jede begrenzte kontinuierliche Funktion kann mit beliebig kleinem Fehler von einem ANN mit einem Hidden Layer abgebildet werden.
Jede begrenzte kontinuierliche Funktion kann mit beliebig kleinem Fehler von einem ANN mit einem Hidden Layer abgebildet werden.
Tags:
Quelle: CI Teil 1 Lecture 4
Quelle: CI Teil 1 Lecture 4
What is credit assignment problem?
In the context of ANN?
In the context of ANN?
Das credit assignment problem ist das Problem herauszufinden welcher Teil eines Systems / Gruppe wieviel zum Erfolg / Misserfolg beigetragen hat.
Im Falle von ANNs geht es darum herauszufinden wieviel jedes Neuron am Fehler 'schuld' ist.
Im Falle von ANNs geht es darum herauszufinden wieviel jedes Neuron am Fehler 'schuld' ist.
Tags:
Quelle: CI Teil 1 Lecture 4
Quelle: CI Teil 1 Lecture 4
What is backpropagation algorithm?
Der backprop. Algorithmus besteht aus 2 Schritten.
Im ersten Schritt wird die Aktivierungsfunktion und der Output z aller Neuronen berechnet.
Im zweiten Schritt wird das Netzwerk vom Output Layer bis zum Input Layer rückwärts durchgegangen und der Fehler jedes einzelnen Neurons berechnet und nach hinten fortgepflanzt.
Im ersten Schritt wird die Aktivierungsfunktion und der Output z aller Neuronen berechnet.
Im zweiten Schritt wird das Netzwerk vom Output Layer bis zum Input Layer rückwärts durchgegangen und der Fehler jedes einzelnen Neurons berechnet und nach hinten fortgepflanzt.
Tags:
Quelle: CI Teil 1 Lecture 4
Quelle: CI Teil 1 Lecture 4
What Error function minimized backpropagation?
Für die Samples wird als Fehlerfunktion die Summe des quadratischen Fehlers verwendet.
E^(i) = 1/2 Summe von k = 0 bis K über (z_k - y_k)^2

E^(i) = 1/2 Summe von k = 0 bis K über (z_k - y_k)^2

Tags:
Quelle: CI Teil 1 Lecture 4
Quelle: CI Teil 1 Lecture 4
Why is backpropagation algorithm used?
Durch die Leistung moderner GPUs ist es backpropagation möglich spitzenresultate zu erziehlen.
Tags:
Quelle: CI Teil 1 Lecture 4
Quelle: CI Teil 1 Lecture 4
Weight update rules for output and hidden neurons?
Fehler für output neurons

Fehler für hidden neurons

Tags:
Quelle: CI Teil 1 Lecture 4
Quelle: CI Teil 1 Lecture 4
What are online and batch learning?
What is the difference?
What is the difference?
Beim online learning wird nach jedem Sample der Fehlergradient berechnet und die Gewichte werden nach jedem Sample aktualisiert.
Beim batch learning werden die Fehelrgradienten aufsummiert und die Gewichte werden nach erst aktualisiert wenn alle Samples gesehen wurden.
Beim batch learning werden die Fehelrgradienten aufsummiert und die Gewichte werden nach erst aktualisiert wenn alle Samples gesehen wurden.
Tags:
Quelle: CI Teil 1 Lecture 4
Quelle: CI Teil 1 Lecture 4
How can one use ANN for classification?
How can one use ANN for regression?
How can one use ANN for regression?
ANN mit einem Hidden Layer.
Aktivierungsfunktion des Hidden Layers muss eine sigmoide Funktion sein.
Wenn die Aktivierungsfunktion im Output Layer ebenfalls eine sigmoide Funktion ist dann implementiert das ANN eine Klassifikation.
Wenn die Aktivierungsfunktion im Output Layer eine lineare Funktion ist dann implementiert das ANN Regression.
Aktivierungsfunktion des Hidden Layers muss eine sigmoide Funktion sein.
Wenn die Aktivierungsfunktion im Output Layer ebenfalls eine sigmoide Funktion ist dann implementiert das ANN eine Klassifikation.
Wenn die Aktivierungsfunktion im Output Layer eine lineare Funktion ist dann implementiert das ANN Regression.
Tags:
Quelle: CI Teil 1 Lecture 4
Quelle: CI Teil 1 Lecture 4
ANN Properties?
- Adaptives model
- Lernrate ist langsam aber testrate ist schnell
- Daten müssen nicht präzise oder perfekt sein
- Resultate hängen nicht von einem einzigen Netzwerkelement ab
- Fehlerresistent (robust / redundant)
- Wissen ist implizit gespeichert
Tags:
Quelle: CI Teil 1 Lecture 4
Quelle: CI Teil 1 Lecture 4
What is the margin of seperation?
The margin of seperatio ist der Bereich um die Entscheidungsgrenze in der sich keine Samples befinden.
Eine große margin of seperation bedeutet eine sehr klare Trennung zwischen den (zwei) Klassen.
Eine große margin of seperation bedeutet eine sehr klare Trennung zwischen den (zwei) Klassen.
Tags:
Quelle: CI Teil 1 Lecture 5
Quelle: CI Teil 1 Lecture 5
What are support vectors?
Supportvektoren sind:
- die nähesten Punkte (samples) zur Entscheidungsgrenze (Hyperebene)
- wichtig für die definition der optimalen Entscheidungsgrenze.
Tags:
Quelle: CI Teil 1 Lecture 5
Quelle: CI Teil 1 Lecture 5
What is SVM?
Support Vector Machine.
Es ist eine lernmethode bei der versucht wird eine optimale Seperationshypereben zu finden bei denen der Normalabstand der nähesten Samples zur Seperationsebene maximiert wird.
Es ist eine lernmethode bei der versucht wird eine optimale Seperationshypereben zu finden bei denen der Normalabstand der nähesten Samples zur Seperationsebene maximiert wird.
Tags:
Quelle: CI Teil 1 Lecture 5
Quelle: CI Teil 1 Lecture 5
What is the seperation hyperplane and the discrimination function?
Die seperationshyperebene ist eine Mehrdimensionale Ebene (eine Dimension weniger als die Daten) mit der form:

Die Diskriminante bestimmt in welche Klasse eine Sample gehört mit der form:
gehört mit der form:


Die Diskriminante bestimmt in welche Klasse eine Sample
 gehört mit der form:
gehört mit der form:
Tags:
Quelle: CI Teil 1 Lecture 5
Quelle: CI Teil 1 Lecture 5
What is the distance of a sample from the hyperplane?
Die Distanz eines Samples zur Hyperebene ist definiert als:

wobei die Euklidische Norm von
die Euklidische Norm von  ist.
ist.

wobei
 die Euklidische Norm von
die Euklidische Norm von  ist.
ist.Tags:
Quelle: CI Teil 1 Lecture 5
Quelle: CI Teil 1 Lecture 5
How is the margin of separation maximized?
Maximizing the margin is equivalent to minimizing  .
.
 .
.Tags:
Quelle: CI Teil 1 Lecture 5
Quelle: CI Teil 1 Lecture 5
Why do we use soft margins?
SVMs funktionieren nur wenn die Daten linear trennbar sind (eventuell über Kernel Funktion).
Um mit Outlieren bzw. falschen Samples (mislabled) umgehen zu können ist die idee eine Slackvariable einzuführen und so auf die wichtigkeit von bestimmter Samples rücksicht nehmen zu können.
Um mit Outlieren bzw. falschen Samples (mislabled) umgehen zu können ist die idee eine Slackvariable einzuführen und so auf die wichtigkeit von bestimmter Samples rücksicht nehmen zu können.
Tags:
Quelle: CI Teil 1 Lecture 5
Quelle: CI Teil 1 Lecture 5
What is a kernel function?
Kernelfunktionen sind funktionen die das innere Produkt zwischen Datenpunkten in einem Raum liefern.
Dadurch kann man in höherdimensionalen Impliziten Räumen arbeiten ohne explizit das mapping zu berechnen.
Dies ist oft schneller als die explizite Berechnung (dies wird als Kernel Trick bezeichnet).
Dadurch kann man in höherdimensionalen Impliziten Räumen arbeiten ohne explizit das mapping zu berechnen.
Dies ist oft schneller als die explizite Berechnung (dies wird als Kernel Trick bezeichnet).
Tags:
Quelle: CI Teil 1 Lecture 5
Quelle: CI Teil 1 Lecture 5
State Cover's theorem
Given a set of training data that is not linearely separable, one can with high probability transform it into a training set that is linearly separable by projecting it into a higher dimension space via non-linear transformation.
Tags:
Quelle: CI Teil 1 Lecture 5
Quelle: CI Teil 1 Lecture 5
What is the kernel trick?
Der Kernel Trick ist die Tatsache das die implizite Rechnung über Kernelfunktionen (Inneres Produkt zwischen Datenpunkten in einem anderen Raum) oft schneller ist als die explizite Berechnung des mappings.
Tags:
Quelle: CI Teil 1 Lecture 5
Quelle: CI Teil 1 Lecture 5
Tags:
Quelle: CI Teil 1 Lecture 5
Quelle: CI Teil 1 Lecture 5
Name a few standard kernels
- Polynomial Kernel

- RBF Kernel

- Sigmoid Kernel

- String kernel
- Graph kernel
Tags:
Quelle: CI Teil 1 Lecture 5
Quelle: CI Teil 1 Lecture 5
Explain the differences between multiclass and multilabel classifiction
Multiclass classification:
Jedes Sample gehört zu genau einer von N Klassen.
Multilable classification:
Jedes Sample hat eine Anzahl von Lables (mehrere Klassen).
Jedes Sample gehört zu genau einer von N Klassen.
Multilable classification:
Jedes Sample hat eine Anzahl von Lables (mehrere Klassen).
Tags:
Quelle: CI Teil 1 Lecture 5
Quelle: CI Teil 1 Lecture 5
Name a few methods for multiclass problems
Entweder classifier die direkt multiclass unterstützen:
oder binäre classifier mit verschiedenen Methoden für Multiclass adaptieren:
- Decision trees
- Naive Bayes
- Multiclass SVM
oder binäre classifier mit verschiedenen Methoden für Multiclass adaptieren:
- One vs. All (OVA)
- One vs. One (OVO)
- Error Correcting Output Codes (ECOC)
Tags:
Quelle: CI Teil 1 Lecture 5
Quelle: CI Teil 1 Lecture 5
What is OVA?
One vs. All
Eine Methode mit der man mittels einem Binären Classifier Multiclass classification realisieren kann.
Dabei werden N Classifier trainiert wobei jeder einzelne Unterscheiden kann ob ein sample x in der Klasse n_i ist oder nicht.
Ein neues Sample wird dann von allen Classifieren einmal klassifiziert und es wird die Klasse mit der höchsten Zuversicht ausgewählt.
Class = arg max h_k ( x^(i))
Eine Methode mit der man mittels einem Binären Classifier Multiclass classification realisieren kann.
Dabei werden N Classifier trainiert wobei jeder einzelne Unterscheiden kann ob ein sample x in der Klasse n_i ist oder nicht.
Ein neues Sample wird dann von allen Classifieren einmal klassifiziert und es wird die Klasse mit der höchsten Zuversicht ausgewählt.
Class = arg max h_k ( x^(i))
Tags:
Quelle: CI Teil 1 Lecture 5
Quelle: CI Teil 1 Lecture 5
OVA vs. OVO
Bei OVA (One vs. All) werden für N Klassen N Klassifier gelernt wobei jeder einen gegen alle anderen testet (ist x in Klasse n oder nicht).
Bei OVO (One vs. One) werden für N Klassen N * (N-1) / 2 Klassifier gelernt wobei jeder Klassifier Entscheidet ob ein Sample in Klasse A, in Klasse B oder weder noch ist.
Am Ende wird ein Sample jener Klasse zugeordnet für die es die meisten Stimmen erhalten hat.
Bei OVO (One vs. One) werden für N Klassen N * (N-1) / 2 Klassifier gelernt wobei jeder Klassifier Entscheidet ob ein Sample in Klasse A, in Klasse B oder weder noch ist.
Am Ende wird ein Sample jener Klasse zugeordnet für die es die meisten Stimmen erhalten hat.
Tags:
Quelle: CI Teil 1 Lecture 5
Quelle: CI Teil 1 Lecture 5
What is ECOC?
Error Correcting Output Codes
Jede Klasse wird durch einen binären Code der Länge n repräsentiert.
Jedes Bit gehört zum Output eines Klassifiers.
1 Klassifier pro Bit.
Nachdem die Klassifier ihren Output produziert haben wird der näheste binärcode gesucht um so die Klasse zu entscheiden (nähe wird euklidische Norm, Manhattan o.a. bestimmt).
Jede Klasse wird durch einen binären Code der Länge n repräsentiert.
Jedes Bit gehört zum Output eines Klassifiers.
1 Klassifier pro Bit.
Nachdem die Klassifier ihren Output produziert haben wird der näheste binärcode gesucht um so die Klasse zu entscheiden (nähe wird euklidische Norm, Manhattan o.a. bestimmt).
Tags:
Quelle: CI Teil 1 Lecture 5
Quelle: CI Teil 1 Lecture 5
What is the confusion matrix and why do we use it?
The confusion matrix tells us how often a sample that should have been x was classified as something different and it tells us what it was classified as.
From this it is easy to see if the classifier confuses two classes.
This can be used to improve the accuracy of the system by introducing new features to the classifier responsible for seperating specific classes.
From this it is easy to see if the classifier confuses two classes.
This can be used to improve the accuracy of the system by introducing new features to the classifier responsible for seperating specific classes.
Tags:
Quelle: CI Teil 1 Lecture 5
Quelle: CI Teil 1 Lecture 5
What are the differences between lazy and eager learning?
Lazy Learning
The system tries to generalize the training data before receiving queries (-> Neural Networks)
Eager Learning:
The system does not generalize until a guery is made to the system (-> k-NN)
The system tries to generalize the training data before receiving queries (-> Neural Networks)
- +target function approximated globally
- +deals with noise in the training data
- -unable to provide good local approximations
Eager Learning:
The system does not generalize until a guery is made to the system (-> k-NN)
- +target function approximated locally
- -large space requirements to store the entire training dataset
- -slow to evaluate
Tags:
Quelle: CI Teil 1 Lecture 6
Quelle: CI Teil 1 Lecture 6
What is Instance based learning?
New problem instances are compared with instances seen in training phase (stored in memory) instead of performing explicit generalization (lazy learning).
Hypothesis
Advantage
Hypothesis
- Constructed on the fly directly from the training instances
- The complexity can grow with the data
- In the worst case it is a list of all training samples
Advantage
- Adapt the model to previous unseen data
Tags:
Quelle: CI Teil 1 Lecture 6
Quelle: CI Teil 1 Lecture 6
What is k-NN?
k-NN stands for k nearest neighbors.
It is one of the simplest machine learning algorithm (instanced based learning).
For a new sample look at the k closest samples (use some distance metric like Euclidean).
Assign the new sample to the most frequent occuring class within those k samples.
It is one of the simplest machine learning algorithm (instanced based learning).
For a new sample look at the k closest samples (use some distance metric like Euclidean).
Assign the new sample to the most frequent occuring class within those k samples.
Tags:
Quelle: CI Teil 1 Lecture 6
Quelle: CI Teil 1 Lecture 6
How does the number of neighbors influence k-NN?
If you only look at a small number of neighbors the decision boundary between classes is very distinct.
A large value of k reduces the effect of noise on the classification but the boundary between classses becomes less distinct.
The best choice of k depends on the data.
A large value of k reduces the effect of noise on the classification but the boundary between classses becomes less distinct.
The best choice of k depends on the data.
Tags:
Quelle: CI Teil 1 Lecture 6
Quelle: CI Teil 1 Lecture 6
Training and testing procedure for k-NN?
Training
Basically non-existing. Store the training samples and maybe perform some preprocessing to speed up queries (feature extraction, dimensionality reduction)
Testing
For classification look at the k nearest neighbors and pick the class with the most votes.
For regression average the values of the k nearest neighbors.
Basically non-existing. Store the training samples and maybe perform some preprocessing to speed up queries (feature extraction, dimensionality reduction)
Testing
For classification look at the k nearest neighbors and pick the class with the most votes.
For regression average the values of the k nearest neighbors.
Tags:
Quelle: CI Teil 1 Lecture 6
Quelle: CI Teil 1 Lecture 6
When to use k-NN and what are pros / cons?
k-NN works best when there is lots of data avaiable and the data has a small amount of features.
Pros:
Cons:
Pros:
- Easy to implement
- Very fast training
- No information loss
- high classification accuracy if lots of data is avaiable
- Intuitive interpretation
- Can have very complex decision boundaries
Cons:
- Requires lots of memory to store all the data samples
- Slow query time
- Sensitive to the local structure of the data
- The parameter k needs to be tuned
Tags:
Quelle: CI Teil 1 Lecture 6
Quelle: CI Teil 1 Lecture 6
What is overfitting and how to deal with it?
Overfitting is the result of an overly complex models where the learned function h(x) essentially 'connects the dots' of the training data.
This results in a low training error but a high test error.
Use model selection to automatically select the right model complexity.
Use regularization to keep parameters small.
This results in a low training error but a high test error.
Use model selection to automatically select the right model complexity.
Use regularization to keep parameters small.
Tags:
Quelle: CI Teil 1 Lecture 6
Quelle: CI Teil 1 Lecture 6
What is a validation set?
A Validation Set is a Set of Data used for model selection.
Model selection takes a number of Hypothesis' and a Validation Set and returns a selected hypothesis with the smallest error on the validation set.
Model selection takes a number of Hypothesis' and a Validation Set and returns a selected hypothesis with the smallest error on the validation set.
Tags:
Quelle: CI Teil 1 Lecture 6
Quelle: CI Teil 1 Lecture 6
What is cross-validation?
Cross validation is the idea to take the avaiable Data and split it into multiple parts and then use some of those parts as the training data and some as validation data. This is done over multiple rounds with the parts used for training and the parts used for validation changing.
This gives us insight on ho wthe model will generalize to an independent dataset in order to limit problems like overfitting.
This gives us insight on ho wthe model will generalize to an independent dataset in order to limit problems like overfitting.
Tags:
Quelle: CI Teil 1 Lecture 6
Quelle: CI Teil 1 Lecture 6
Types of cross-validation?
- k-fold Split the data into k parts. Use k-1 parts for Training and the last for validation. Repeat k times.
- 2-fold Split the data into 2 parts. Use each part once for training and validate with the other.
- Leave-one-out Split the data into as many parts as you have data points. Train with all but one and validate with the one left out.
- Repeated random sub-sampling Split the dataset randomly k times. Choose independantly how large each validation set is.
Tags:
Quelle: CI Teil 1 Lecture 6
Quelle: CI Teil 1 Lecture 6
Difference between 2-fold and leave-one-out cross-validation?
2-fold is the simplest methode where the data is split into two equal parts.
Train on the first fold and validate on the second and vice versa.
Leave-one-out cross-validation splits the data into k equal parts where k is the number of samples in the training set.
Use a single sample as a validatoin set and all the rest as training set (k times).
Train on the first fold and validate on the second and vice versa.
Leave-one-out cross-validation splits the data into k equal parts where k is the number of samples in the training set.
Use a single sample as a validatoin set and all the rest as training set (k times).
Tags:
Quelle: CI Teil 1 Lecture 6
Quelle: CI Teil 1 Lecture 6
What is the bias-variance tradeoff?
Bias is how accurate a model is across different training sets (how general a model is).
Variance is how sensitive a model is to small changes in the training set.
Error = Variance + Bias^2 + Noise
We want to minimize the bias and the variance of the model error.
High bias -> underfitting (model too simple)
High variance -> overfitting (model too complex)
To achieve good performance on data outside the training set a tradeoff must be made.
Variance is how sensitive a model is to small changes in the training set.
Error = Variance + Bias^2 + Noise
We want to minimize the bias and the variance of the model error.
High bias -> underfitting (model too simple)
High variance -> overfitting (model too complex)
To achieve good performance on data outside the training set a tradeoff must be made.
Tags:
Quelle: CI Teil 1 Lecture 6
Quelle: CI Teil 1 Lecture 6
What is regularization and how is it used?
Regularization is a system to penalize models with extreme parameters values.
instead of minimizing the cost function we minimize
we minimize 
instead of minimizing the cost function
 we minimize
we minimize 
Tags:
Quelle: CI Teil 1 Lecture 6
Quelle: CI Teil 1 Lecture 6
Tags:
Quelle: CI Teil 1 Lecture 6
Quelle: CI Teil 1 Lecture 6
Nennen und beschreiben sie die 3 Arten des Lernens
Überwachtes Lernen
Gegeben sind Daten x_1 ... x_n und Zielwerte t_1 ... t_n
Unüberwachtes Lernen
Hier sind nur Daten x_1 ... x_n gegeben aber keine Zielwerte. (z.b. Maximum-Likelihood Schätzer, Bayes Schätzer)
Reinforcement Lernen
Lernen ohne unmittelbare Rückmeldung ob die Zwischenschritte korrekt sind, nur das Resultat wird bewertet (z.b. Roboter sucht Würfel, feedback erst nachdem er das Objekt gefunden hat).
Gegeben sind Daten x_1 ... x_n und Zielwerte t_1 ... t_n
Unüberwachtes Lernen
Hier sind nur Daten x_1 ... x_n gegeben aber keine Zielwerte. (z.b. Maximum-Likelihood Schätzer, Bayes Schätzer)
Reinforcement Lernen
Lernen ohne unmittelbare Rückmeldung ob die Zwischenschritte korrekt sind, nur das Resultat wird bewertet (z.b. Roboter sucht Würfel, feedback erst nachdem er das Objekt gefunden hat).
Tags:
Quelle: CI Teil 2 Kapitel 1
Quelle: CI Teil 2 Kapitel 1
Tags:
Quelle: CI Teil 2 Kapitel 1
Quelle: CI Teil 2 Kapitel 1
Tags:
Quelle: CI Teil 2 Kapitel 1
Quelle: CI Teil 2 Kapitel 1
Erklären sie den Bayes Klassifikator
Die Klassifikation erfolgt anhand der Warscheinlichkeit für Klasse t gegeben die Objektbeschreibung x. d.h. P(t | x) ist notwendig.
Wenn z.b. P(t = 1 | x) > P(t = 2 | x) ist dann wählt man Klasse 1.
Die posterior Wahrscheinlichkeit kann über den Satz von Bayes formuliert werden.

P(x | t) ... Likelihood
P(t) ... prior Wahrscheinlichkeit
P(t | x) ... posterior Wahrscheinlichkeit
Wenn z.b. P(t = 1 | x) > P(t = 2 | x) ist dann wählt man Klasse 1.
Die posterior Wahrscheinlichkeit kann über den Satz von Bayes formuliert werden.

P(x | t) ... Likelihood
P(t) ... prior Wahrscheinlichkeit
P(t | x) ... posterior Wahrscheinlichkeit
Tags:
Quelle: CI Teil 2 Kapitel 3
Quelle: CI Teil 2 Kapitel 3
Erklären sie den Begriff iid
iid steht für independent identically distributed
idd heißt, dass die Samples x_1,...,x_n statistisch unabhängig sind und von der gleichen Wahrscheinlichkeitsverteilung stammen.
idd heißt, dass die Samples x_1,...,x_n statistisch unabhängig sind und von der gleichen Wahrscheinlichkeitsverteilung stammen.
Tags:
Quelle: CI Teil 2 Kapitel 2
Quelle: CI Teil 2 Kapitel 2
Erklären sie den EM-Algorithmus
Der EM-Algorithmus ist ein iterative Algorithmus zum Lernen von Gaußschen Mischverteilungen.
Zuerst werden die Parameter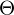 initialisiert.
initialisiert.
Im E-Step können auf Grund der Parameter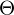 die Zugehörigkeitswahrscheinlichkeiten
die Zugehörigkeitswahrscheinlichkeiten  berechnet werden.
berechnet werden.
Im M-Step (maximierender Schritt) werden die Parameter und
und  unter Zuhilfename von
unter Zuhilfename von  neu berechnet.
neu berechnet.
Der E und der M-Step werden abwechselnd durchgeführt bis die log-Likelihood-Funktion konvertgiert.
konvertgiert.
1. Initialisierung
2. E-Step: Klassenzugehörigkeit ausrechnen

3. M-Step: Berechnen der Parameter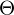
4. Evaluieren

-> falls konvergiert Abbruch
-> falls nicht konvergiert => E-Step
Zuerst werden die Parameter
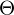 initialisiert.
initialisiert.Im E-Step können auf Grund der Parameter
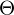 die Zugehörigkeitswahrscheinlichkeiten
die Zugehörigkeitswahrscheinlichkeiten  berechnet werden.
berechnet werden.Im M-Step (maximierender Schritt) werden die Parameter
 und
und  unter Zuhilfename von
unter Zuhilfename von  neu berechnet.
neu berechnet.Der E und der M-Step werden abwechselnd durchgeführt bis die log-Likelihood-Funktion
 konvertgiert.
konvertgiert.1. Initialisierung
2. E-Step: Klassenzugehörigkeit ausrechnen

3. M-Step: Berechnen der Parameter
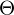
4. Evaluieren

-> falls konvergiert Abbruch

-> falls nicht konvergiert => E-Step
Tags:
Quelle: CI Teil 2 Kapitel 4
Quelle: CI Teil 2 Kapitel 4
Eigenschaften des EM Algorithmus
- Die log-Likelihood
 wird in der Regel mit jeder Iteration monoton größer.
wird in der Regel mit jeder Iteration monoton größer. - Der EM Algorithmus findet ein kokales Optima d.h. ein lokales Maximum der Likelihood Funktion. Wenn es mehrere lokale Maxima gibt, wird das globale Optimim in der Regel nicht gefunden.
- Die Lösung hängt von der Initialisierung von
 ab.
ab.
Tags:
Quelle: CI Teil 2 Kapitel 4
Quelle: CI Teil 2 Kapitel 4
Erklären sie den K-means Algorithmus
Das Ziel von K-means ist es die Daten in Cluster einzuteilen.
K ist dabei die Anzahl der Cluster.
Der K-means Algorithmus ist eine modifikation des EM-Algorithmus für Gaussian Mixture Models (GMMs).
Unterschiede zwischen EM und K-means:
K ist dabei die Anzahl der Cluster.
Der K-means Algorithmus ist eine modifikation des EM-Algorithmus für Gaussian Mixture Models (GMMs).
Unterschiede zwischen EM und K-means:
-
 d.h.
d.h.  kann vernachlässigt werden da es nicht modifiziert wird.
kann vernachlässigt werden da es nicht modifiziert wird. - Es werden alle Komponenten durch die gleiche sphärische Kovarianzmatrix dargestellt.

- Jedes Sample wird von einer Komponente modelliert.
Tags:
Quelle: CI Teil 2 Kapitel 5
Quelle: CI Teil 2 Kapitel 5
Funktionsweise von K-means
1. Initialisierung: Wähle K Samples zufällig für die Clusterzentren aus
2. Step 1: Klassifikation der Samples zu den Komponenten
3. Step 2: Neuberechnung der Mittelwertvektoren (Schwerpunkt der Cluster)
4. Evaluierung der kumulativen Distanz
falls Distanz konvergiert dann sind die optimalen Clusterzentren gefunden
falls Distanz nicht konvergiert => Step 1
2. Step 1: Klassifikation der Samples zu den Komponenten
3. Step 2: Neuberechnung der Mittelwertvektoren (Schwerpunkt der Cluster)
4. Evaluierung der kumulativen Distanz
falls Distanz konvergiert dann sind die optimalen Clusterzentren gefunden
falls Distanz nicht konvergiert => Step 1
Tags:
Quelle: CI Teil 2 Kapitel 5
Quelle: CI Teil 2 Kapitel 5
Nennen sie 4 Eigenschaften von K-means
- K-means konvergiert zu lokalem Minimum der kumulativen Distanz
- Mit jeder Iteration wird die kumulative Distanz kleiner
- Ergebnis ist von der Initialisierung von
 abhängig. d.h. es wird in der Regel kein globales Optimum gefunden.
abhängig. d.h. es wird in der Regel kein globales Optimum gefunden. - Entscheidungsgrenzen zwischen den Clustern sind stückweise linear.
Tags:
Quelle: CI Teil 2 Kapitel 5
Quelle: CI Teil 2 Kapitel 5
Nennen und beschreiben sie 3 Grammatikmodelle für die Spracherkennung mittels Markov Modell (MM)
Unigramm Grammatik Modell
Hier wird die Anname getroffen, dass keine Abängigkeit zwischen den Wörtern besteht. d.h. die Wörter sind iid.
Das Problem ist das P(Ich gehe einkaufen) = P(einkaufen ich gehe) ist. Grammatikalisch richtige haben also keine höhere Wahrscheinlichkeit als gramatikalisch falsche.
Bigramm Modell
Hier handel es sich um ein Markov Modell 1. Ordnung. Hier wird jeweils das Anfangswort und die Übergangswahrscheinchkeit zwischen einem Wort und seinem Nachfolger berücksichtigt.
Trigramm Modell
Dies ist ein Markov Modell 2. Ordnung, der Kontext wird auf 2 vorangegangene States ausgeweitet, wärend bei einem Markov Modell 1. Ordnung nur ein vorgegangener State berücksichtigt wird.
Hier wird die Anname getroffen, dass keine Abängigkeit zwischen den Wörtern besteht. d.h. die Wörter sind iid.
Das Problem ist das P(Ich gehe einkaufen) = P(einkaufen ich gehe) ist. Grammatikalisch richtige haben also keine höhere Wahrscheinlichkeit als gramatikalisch falsche.
Bigramm Modell
Hier handel es sich um ein Markov Modell 1. Ordnung. Hier wird jeweils das Anfangswort und die Übergangswahrscheinchkeit zwischen einem Wort und seinem Nachfolger berücksichtigt.
Trigramm Modell
Dies ist ein Markov Modell 2. Ordnung, der Kontext wird auf 2 vorangegangene States ausgeweitet, wärend bei einem Markov Modell 1. Ordnung nur ein vorgegangener State berücksichtigt wird.
Tags:
Quelle: CI Teil 2 Kapitel 6
Quelle: CI Teil 2 Kapitel 6
Beschreiben sie das Markov Modell
Wofür ist es geeignet, zu welchem Problem kann es dabei kommen und wie bekommt man dies unter Kontrolle?
Wofür ist es geeignet, zu welchem Problem kann es dabei kommen und wie bekommt man dies unter Kontrolle?
Das Markov Modell ist zur Modellierung von Sequenzen geeignet, d.h. es modelliert explizit die Abhängigkeit zwischen den Samples.
Die iid Anname wird zum Teil vernachlässigt.
Das Markov Modell besteht aus einer Menge der Zustände, den Anfangswahrscheinlichkeiten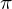 und den Übergangswahrscheinlichkeiten
und den Übergangswahrscheinlichkeiten  .
.
Die Übergangswahrscheinlichkeiten sind in der Übergangsmatrix A zusammengefasst.
Ein Problem für das Markov Modell ist die Tatsache das die Anzahl an Wahrscheinlichkeiten exponentiell mit der Satzlänge N steigt. Bei 1000 States (z.b. Wörter) und einer Satzlänger von N= 10 gibt es bereits 1000^10 Wahrscheinlichkeiten.
Durch das Einführen des Kontext kann man sich hier abhilfe schaffen. Dbaei werden nur Sequenzen bestimmter länger zusammen bewertet.
Die iid Anname wird zum Teil vernachlässigt.
Das Markov Modell besteht aus einer Menge der Zustände, den Anfangswahrscheinlichkeiten
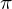 und den Übergangswahrscheinlichkeiten
und den Übergangswahrscheinlichkeiten  .
.Die Übergangswahrscheinlichkeiten sind in der Übergangsmatrix A zusammengefasst.
Ein Problem für das Markov Modell ist die Tatsache das die Anzahl an Wahrscheinlichkeiten exponentiell mit der Satzlänge N steigt. Bei 1000 States (z.b. Wörter) und einer Satzlänger von N= 10 gibt es bereits 1000^10 Wahrscheinlichkeiten.
Durch das Einführen des Kontext kann man sich hier abhilfe schaffen. Dbaei werden nur Sequenzen bestimmter länger zusammen bewertet.
Tags:
Quelle: CI Teil 2 Kapitel 6
Quelle: CI Teil 2 Kapitel 6
Erklären sie das Hidden Markov Modell (HMM)
Im Unterschied zum Markov Modell ist beim Hidden Markov Modell der State nicht direkt beobachtbar (=hidden).
Es gibt aber Beobachtungen X_n die stochastisch mit dem State Q_n zum selben Zeitpunkt n zusammenhängen.
Das HMM hat zusätzlich zu den Parametern des MMs noch die Beobachtungswahrscheinlichkeit B.

Desweiteren gilt das die Beobachtung nur zum State
nur zum State  abhängt.
abhängt.
Es gibt aber Beobachtungen X_n die stochastisch mit dem State Q_n zum selben Zeitpunkt n zusammenhängen.
Das HMM hat zusätzlich zu den Parametern des MMs noch die Beobachtungswahrscheinlichkeit B.

Desweiteren gilt das die Beobachtung
 nur zum State
nur zum State  abhängt.
abhängt.Tags:
Quelle: CI Teil 2 Kapitel 7
Quelle: CI Teil 2 Kapitel 7
Kartensatzinfo:
Autor: Sepp Samuel
Oberthema: Telematik
Thema: Computational Intelligence
Schule / Uni: TU Graz
Veröffentlicht: 02.07.2014
Schlagwörter Karten:
Alle Karten (92)
keine Schlagwörter







