Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
27
Simulation TM durch RAM
Simulation einer 1-Band-TM als RAM:
- Register 1 speichert den Index der Kopfposition
- Register 2 speichert aktuellen Zustand
- Register 3,4,... speichern Inhalte der Bandpositionen 0,1,2,... falls diese zur Eingabe der TM gehören oder vorher vom Kopf besucht wurden
Rechenschritte:
1.) Überprüfung, ob TM im aktuellen Schritt terminiert (falls ja, endet RAM mit entsprechender Ausgabe)
2.) erste Stufe: |Q| viele IF-Abfragen: aktuellen Zustand bestimmen
zweite Stufe: |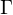
| viele IF-Abfragen: gelesenes Zeichen bestimmen
=> je nach Ausgang der IF-Anfragen wird der Zustand in Register 2 und die Kopfposition in Register 1 und das Zeichen an Bandposition c(1) geändert
Laufzeit:
uniformes Kostenmaß: O(n+t(n))
logarithmisches Kostenmaß: Zustände in Zeichen haben konstante Kodierungslänge. Bandpos, die angesprochen werden sind durch n+t(n) beschränkt. Kodierungslänge der Position ist also O(log(n+t(n)). Insgesamt also: O((t(n) + n)log(t(n) + n)
- Register 1 speichert den Index der Kopfposition
- Register 2 speichert aktuellen Zustand
- Register 3,4,... speichern Inhalte der Bandpositionen 0,1,2,... falls diese zur Eingabe der TM gehören oder vorher vom Kopf besucht wurden
Rechenschritte:
1.) Überprüfung, ob TM im aktuellen Schritt terminiert (falls ja, endet RAM mit entsprechender Ausgabe)
2.) erste Stufe: |Q| viele IF-Abfragen: aktuellen Zustand bestimmen
zweite Stufe: |
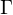| viele IF-Abfragen: gelesenes Zeichen bestimmen=> je nach Ausgang der IF-Anfragen wird der Zustand in Register 2 und die Kopfposition in Register 1 und das Zeichen an Bandposition c(1) geändert
Laufzeit:
uniformes Kostenmaß: O(n+t(n))
logarithmisches Kostenmaß: Zustände in Zeichen haben konstante Kodierungslänge. Bandpos, die angesprochen werden sind durch n+t(n) beschränkt. Kodierungslänge der Position ist also O(log(n+t(n)). Insgesamt also: O((t(n) + n)log(t(n) + n)
