Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
21
Ich gebe Ihnen zwei Fotos. Wie funktioniert damit der 8 Punkte Algorithmus? bzw. Wie kann man die F-Matrix schätzen?
1. mindestens 8 linear unabhängige (nicht auf einer Linie liegende) Punktkorrespondezen in beiden Bildern finden
2. F-Matrix mit Hilfe des 8-Punkte-Algorithmus schätzen
Jedes Punktepaar / jede Punktkorrespondenz liefert eine Gleichung der Form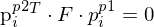 , mit
, mit 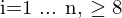
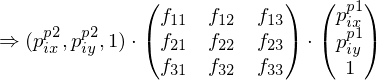
... Umformen bis alles in einer Zeile steht (siehe Skript Ameling) .
Dann f-Werte aus Gleichungen herausnehmen und in LGS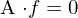 umformen.
umformen.
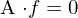
Somit ist f der Nullraum von A und kann mittels SVD bestimmt werden.
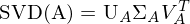
Durch Rauschen kann A auch einen Rang größer 8, also 9 haben. Der Nullraum ergibt sich aus der Spalte von V korrespondierend zum kleinsten Singulärewert von A. Dabei ist F nur bis auf einen Skalierungsfaktor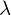 eindeutig.
eindeutig.

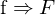
Es muss sichergestellt werden, dass F den Rang zwei hat (Eigenschaft der beinhalteten E-Matrix). Der Rang kann durch die SVD erzwungen werden.
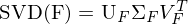
Nun wird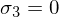 gesetzt und die F-Matrix neu berechnet:
gesetzt und die F-Matrix neu berechnet:
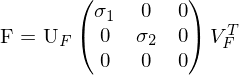
Der Algorithmus ist numerisch instabil. Zur Stabilisierung können die Koordinaten normalisiert werden, so dass die Einträge von A in einer vergleichbaren Größe stabil sind.
- kann manuell geschehen oder
- durch Merkmalsdetektion (Gradienten, Ecken, Features, ...)
2. F-Matrix mit Hilfe des 8-Punkte-Algorithmus schätzen
- F-Matrix kann bis auf einen Skalierungsfaktor
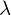 eindeutig bestimmt werden (dieser Skalierungsfaktor bestimmt das eigentliche Größenverhältnis (z.B. wieviel Millimeter entsprechen einem Pixel) ... wid in Kalibrierung/Kameramodell bestimmt
eindeutig bestimmt werden (dieser Skalierungsfaktor bestimmt das eigentliche Größenverhältnis (z.B. wieviel Millimeter entsprechen einem Pixel) ... wid in Kalibrierung/Kameramodell bestimmt - je mehr Punktkorrespondenzen
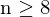 zur Verfügung stehen, desto stabiler wird das Ergebnis
zur Verfügung stehen, desto stabiler wird das Ergebnis
Jedes Punktepaar / jede Punktkorrespondenz liefert eine Gleichung der Form
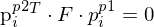 , mit
, mit 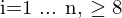
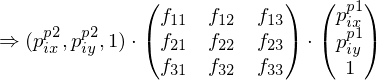
... Umformen bis alles in einer Zeile steht (siehe Skript Ameling) .
Dann f-Werte aus Gleichungen herausnehmen und in LGS
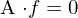 umformen.
umformen. - für jede Punktkorrespondenz entsteht eine Zeile in A
- Anzahl der Spalten von A ist 9 (Werte der F-Matrix)
- die 9 Werte der F-Matrix stehen im Spaltenvektor f
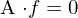
Somit ist f der Nullraum von A und kann mittels SVD bestimmt werden.
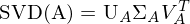
Durch Rauschen kann A auch einen Rang größer 8, also 9 haben. Der Nullraum ergibt sich aus der Spalte von V korrespondierend zum kleinsten Singulärewert von A. Dabei ist F nur bis auf einen Skalierungsfaktor
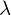 eindeutig.
eindeutig.
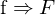
Es muss sichergestellt werden, dass F den Rang zwei hat (Eigenschaft der beinhalteten E-Matrix). Der Rang kann durch die SVD erzwungen werden.
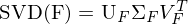
Nun wird
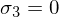 gesetzt und die F-Matrix neu berechnet:
gesetzt und die F-Matrix neu berechnet: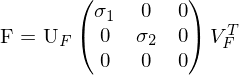
Der Algorithmus ist numerisch instabil. Zur Stabilisierung können die Koordinaten normalisiert werden, so dass die Einträge von A in einer vergleichbaren Größe stabil sind.
Karteninfo:
Autor: CoboCards-User
Oberthema: Rechnsersehen
Thema: Epipolargeometrie
Veröffentlicht: 05.11.2010

