Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
44
Warum hat eine ganzrationale Funktion vom Grad n höchstens n Nullstellen?
Jede Nullstelle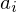 
einer ganzrationalen Funktion erzeugt in der Produktform einen Linearfaktor der Form 
.
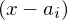Gäbe es mehr als n Nullstellen, könnte man die Funktion in der Produktdarstellung mit mehr als n Linearfaktoren darstellen. Beim Ausmultiplizieren wäre hierbei die größte x-Potenz größer als n. Das kann nicht sein.
Beachte: Es gibt natürlich ganzrationale Funktionen vom Grad n mit weniger als n Nullstellen.
Beispiel: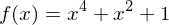
hat gar keine Nullstelle.
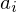einer ganzrationalen Funktion erzeugt in der Produktform einen Linearfaktor der Form 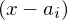. Gäbe es mehr als n Nullstellen, könnte man die Funktion in der Produktdarstellung mit mehr als n Linearfaktoren darstellen. Beim Ausmultiplizieren wäre hierbei die größte x-Potenz größer als n. Das kann nicht sein.
Beachte: Es gibt natürlich ganzrationale Funktionen vom Grad n mit weniger als n Nullstellen.
Beispiel:
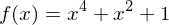hat gar keine Nullstelle.Tags: ganzrational, Grad, Nullstelle
Quelle:
Quelle:
Karteninfo:
Autor: www.mathematik-bw.de
Oberthema: Mathematik
Thema: 10. Klasse
Schule / Uni: Clara-Schumann-Gymnasium
Ort: Lahr
Veröffentlicht: 23.12.2009