Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
28
Diagonalisierbarkeit einer Matrix 

Ist eine Matrix  diagonalisierbar, existiert eine Diagonalmatrix
diagonalisierbar, existiert eine Diagonalmatrix  für die die Ähnlichkeitsbedingung erfüllt ist:
für die die Ähnlichkeitsbedingung erfüllt ist:

Äquivalent: (Vielleicht selbst zu zeigen!?)
Dies ist genau dann wenn: (a) char. Pol. vollständig in Linearfaktoren zerfällt und (b) für alle
für alle 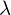 also Eigenwerte von
also Eigenwerte von  .
.
 diagonalisierbar, existiert eine Diagonalmatrix
diagonalisierbar, existiert eine Diagonalmatrix  für die die Ähnlichkeitsbedingung erfüllt ist:
für die die Ähnlichkeitsbedingung erfüllt ist:
Äquivalent: (Vielleicht selbst zu zeigen!?)
Dies ist genau dann wenn: (a) char. Pol. vollständig in Linearfaktoren zerfällt und (b)
 für alle
für alle 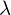 also Eigenwerte von
also Eigenwerte von  .
.
