Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
57
Beweis: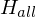 
ist nicht rekursiv aufzählbar
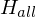ist nicht rekursiv aufzählbar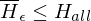
w Eingabe für
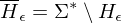
1.) Wenn w keine gültige GN ist, liegt w in
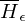. Setze f(w)=w' mit w'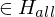 
2.) Wenn w=<M>, so ist f(w)=<M'>. M' verhält sich auf Eingabe x wie folgt:
Falls |x|=i, simuliert M' die ersten i Schritte von M auf
. Wenn M nach i Schritten hält, dann geht M' in eine Endlosschleife, ansonsten hält M'. (d.h. wenn M auf hält liegt M nicht in 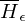und M' darf damit nie halten).f ist offensichtlich berechenbar.Falls w=<M> gilt:
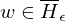
=> M hält nicht auf Eingabe
=>
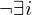: M hält innerhalb von i Schritten auf =>
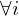: M' hält auf allen Eingaben der Länge i=> f(w)=<M'>
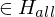
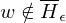
=> M hält auf Eingabe
=>
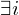: M hält innerhalb von i Schritten auf =>
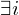: M' hält nicht auf allen Eingaben der Länge i=> f(w)=<M'>
