This flashcard is just one of a free flashcard set. See all flashcards!
32
How are rotations represented by quaternions?
Quaternions are hypercomplex numbers
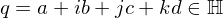
where
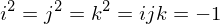
We define the conjugate
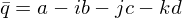
the dot product
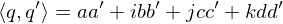
and the norm
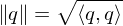
By associating quaternions with vectors in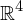 , the product of two quaternions
, the product of two quaternions  ,
,  can be written as a matrix-vector product
can be written as a matrix-vector product
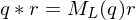
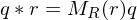
From the structure of these matrices, we can show the dot product equivalence
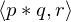
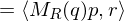
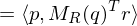
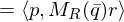
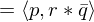
We can embed points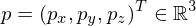 into
into 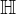 as follows:
as follows:
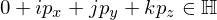
It can be shown that unit quaternions represent rotations. In particular, given a rotation axis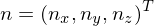 where
where 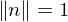 and an angle
and an angle 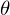 , we can construct
, we can construct
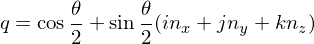
Then, this rotation can be computed as
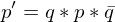
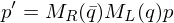
Note that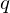 and
and 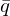 represent the same rotation since both the rotation axis as the magnitude are inverted.
represent the same rotation since both the rotation axis as the magnitude are inverted.
It turns out that
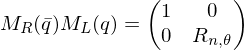
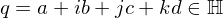
where
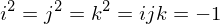
We define the conjugate
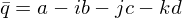
the dot product
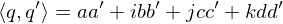
and the norm
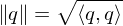
By associating quaternions with vectors in
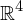 , the product of two quaternions
, the product of two quaternions 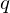 ,
, 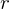 can be written as a matrix-vector product
can be written as a matrix-vector product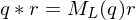
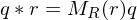
From the structure of these matrices, we can show the dot product equivalence
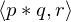
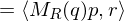
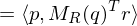
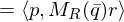
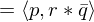
We can embed points
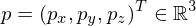 into
into 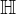 as follows:
as follows: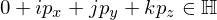
It can be shown that unit quaternions represent rotations. In particular, given a rotation axis
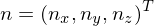 where
where 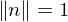 and an angle
and an angle 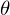 , we can construct
, we can construct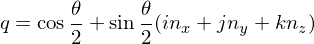
Then, this rotation can be computed as
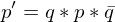
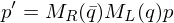
Note that
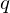 and
and 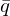 represent the same rotation since both the rotation axis as the magnitude are inverted.
represent the same rotation since both the rotation axis as the magnitude are inverted.It turns out that
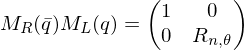
Flashcard info:
Author: janisborn
Main topic: Informatik
Topic: Computergrafik
School / Univ.: RWTH Aachen
City: Aachen
Published: 18.05.2022

