This flashcard is just one of a free flashcard set. See all flashcards!
18
H4: Den Abstand eines Punktes P zu einer Geraden g berechnen
Überlegung:
Zur Hilfe wird eine Ebene E, die orthogonal zur Geraden g ist und den Punkt P enthält aufgestellt. Der Richtungsvektor der Geraden wird dabei als Normalenvektor der Hilfsebene verwendet. Der Schnittpunkt von Gerade und Hilfsebene ist der Lotfußpunkt F. Die Länge der Strecke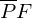 ist der gesuchte Abstand.
ist der gesuchte Abstand.
Die Ebene wird beschrieben durch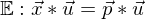 Der gemeinsame Punkt von g und \mathbb E muss beide Gleichungen erfüllen, d.h. es muss gelten:
Der gemeinsame Punkt von g und \mathbb E muss beide Gleichungen erfüllen, d.h. es muss gelten:
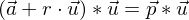
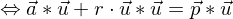
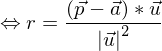
Dieser Wert für r wird in die Parameterdarstellung von g eingesetzt und man erhät die Koordinaten des Lotfußpunktes. Mit der Berechung der Länge der Strecke ist der gesuchte Abstand bestimmt.
ist der gesuchte Abstand bestimmt.
Zur Hilfe wird eine Ebene E, die orthogonal zur Geraden g ist und den Punkt P enthält aufgestellt. Der Richtungsvektor der Geraden wird dabei als Normalenvektor der Hilfsebene verwendet. Der Schnittpunkt von Gerade und Hilfsebene ist der Lotfußpunkt F. Die Länge der Strecke
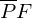 ist der gesuchte Abstand.
ist der gesuchte Abstand.Die Ebene wird beschrieben durch
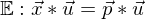 Der gemeinsame Punkt von g und \mathbb E muss beide Gleichungen erfüllen, d.h. es muss gelten:
Der gemeinsame Punkt von g und \mathbb E muss beide Gleichungen erfüllen, d.h. es muss gelten: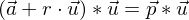
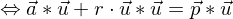
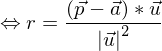
Dieser Wert für r wird in die Parameterdarstellung von g eingesetzt und man erhät die Koordinaten des Lotfußpunktes. Mit der Berechung der Länge der Strecke
 ist der gesuchte Abstand bestimmt.
ist der gesuchte Abstand bestimmt. Flashcard info:
Author: Exinator
Main topic: Mathematik
Topic: Abiturvorbereitung
School / Univ.: MGS
City: Schwelm
Published: 28.03.2011

