Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
38
Faktorieller Ring
Ein Ring  heißt faktoriell, wenn
heißt faktoriell, wenn  integer ist und die äquivalenten Eigenschaften aus Theorem 4.5 besitzt, also:
integer ist und die äquivalenten Eigenschaften aus Theorem 4.5 besitzt, also:
(i) Jede Nicht-Einheit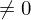 in
in  ist ein (endliches) Produkt von Primelementen
ist ein (endliches) Produkt von Primelementen
(ii) Jede Nicht-Einheit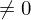 in
in  ist ein (endliches) Produkt aus irreduziblem Elementen und diese Darstellung ist Eindeutig bis auf Reihenfolge und Assoziertheit.
ist ein (endliches) Produkt aus irreduziblem Elementen und diese Darstellung ist Eindeutig bis auf Reihenfolge und Assoziertheit.
(iii) Es gibt keine unendlichen Teilerketten in und je zwei Elemente
und je zwei Elemente 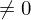 in
in  besitzen einen
besitzen einen 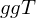 .
.
(iv) Es gibt keine unendlichen Teilerketten in und jedes irreduzible Element ist prim.
und jedes irreduzible Element ist prim.
 heißt faktoriell, wenn
heißt faktoriell, wenn  integer ist und die äquivalenten Eigenschaften aus Theorem 4.5 besitzt, also:
integer ist und die äquivalenten Eigenschaften aus Theorem 4.5 besitzt, also:(i) Jede Nicht-Einheit
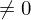 in
in  ist ein (endliches) Produkt von Primelementen
ist ein (endliches) Produkt von Primelementen(ii) Jede Nicht-Einheit
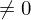 in
in  ist ein (endliches) Produkt aus irreduziblem Elementen und diese Darstellung ist Eindeutig bis auf Reihenfolge und Assoziertheit.
ist ein (endliches) Produkt aus irreduziblem Elementen und diese Darstellung ist Eindeutig bis auf Reihenfolge und Assoziertheit.(iii) Es gibt keine unendlichen Teilerketten in
 und je zwei Elemente
und je zwei Elemente 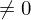 in
in  besitzen einen
besitzen einen 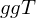 .
.(iv) Es gibt keine unendlichen Teilerketten in
 und jedes irreduzible Element ist prim.
und jedes irreduzible Element ist prim.
