Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
59
Hilberts zehntes Problem
Beschreibe einen Algorithmus, der entscheidet, ob ein gegebenes Polynom mit ganzzahligen Koeffizienten eine ganzzahlige Nullstelle hat
N = {p / p ist ein Polynom mit einer ganzzahligen Nullstelle}
ist rekursiv aufzählbar:
Polynom p mit l Variablen (Wertbereich ist also abzählbar unendliche Menge aller l-Tupel mit Werten in Z: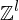
)
Zähle nun nacheinander alle l-Tupel auf und werte p für dieses Tupel aus
Akzeptiere falls Auswertung Null ergibt
=> N wird erkannt
ist nicht rekursiv:
Falls es obere Schranke für Absolutwerte der Nullstellen gebe, müsste man nur endlich viele l-Tupel aufzählen und N wäre rekursiv Dies gilt allerdings nur für Polynome mit einer Variablen:
Für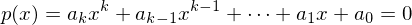
mit ganzzahligen Koeffizienten gitl: 
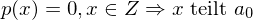. Es gibt also keine Nullstelle mit Absolutwert größer als |a0|.
N = {p / p ist ein Polynom mit einer ganzzahligen Nullstelle}
ist rekursiv aufzählbar:
Polynom p mit l Variablen (Wertbereich ist also abzählbar unendliche Menge aller l-Tupel mit Werten in Z:
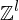)Zähle nun nacheinander alle l-Tupel auf und werte p für dieses Tupel aus
Akzeptiere falls Auswertung Null ergibt
=> N wird erkannt
ist nicht rekursiv:
Falls es obere Schranke für Absolutwerte der Nullstellen gebe, müsste man nur endlich viele l-Tupel aufzählen und N wäre rekursiv Dies gilt allerdings nur für Polynome mit einer Variablen:
Für
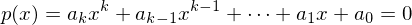mit ganzzahligen Koeffizienten gitl: 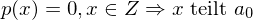. Es gibt also keine Nullstelle mit Absolutwert größer als |a0|.