Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
63
Was beschreibt die Basistransformation?
Der CIE-Normfarbraum ist definiert durch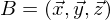 
. Das ist die Basis.
Jede Linearkombination der Basisvektoren mit reellen Zahlen liefert wieder eine Basis dieses Farbraums, insfern die neuen Basisvektoren linear unabhaengig sind.
--> Das kann erreicht werden in dem wir mit einer nicht-singulaeren, linearen 3x3 Matrix
multiplizieren.
Jede Basis liefert ein eigenes Koordinatensystem, wobei der gleiche Vektroraum aufgespannt wird (die lineare Hueller ist identisch)
Es veraendern sich aber Koordinaten bei der Ueberfuehrung.
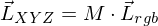
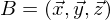. Das ist die Basis.Jede Linearkombination der Basisvektoren mit reellen Zahlen liefert wieder eine Basis dieses Farbraums, insfern die neuen Basisvektoren linear unabhaengig sind.
--> Das kann erreicht werden in dem wir mit einer nicht-singulaeren, linearen 3x3 Matrix
multiplizieren.Jede Basis liefert ein eigenes Koordinatensystem, wobei der gleiche Vektroraum aufgespannt wird (die lineare Hueller ist identisch)
Es veraendern sich aber Koordinaten bei der Ueberfuehrung.
