Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
73
Welche Eigenschaften hat die Fourier-Transformation?

Symmetrie:
Um den Urpsrung symmetrisch
Linearität:
Die Fourier-Transformation ist eine lineare Operation (w = Frequenz)
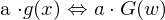
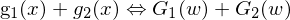
Ähnlichkeit:
Wird die ursprüngliche Funktion g(x) in Zeit oder Raum skaliert, so tritt der entgegengesetzte Effekt im zugehörigen Fourier-Spektrum auf.
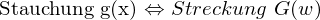
Verschiebungseigenschaft:
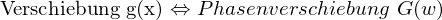
Faltungseigenschaft:
Eine Multiplikation der Funktion in einem Raum (Orts- oder Spektralraum) entspricht einer linearen Faltung (
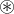 ) der zugehörigen Transformation im jeweils anderen Raum.
) der zugehörigen Transformation im jeweils anderen Raum.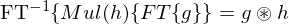
Karteninfo:
Autor: JanBo
Oberthema: Digitale Bildverarbeitung
Thema: Mustererkennung
Schule / Uni: Universität Koblenz-Landau
Ort: Koblenz
Veröffentlicht: 13.09.2012

