This flashcard is just one of a free flashcard set. See all flashcards!

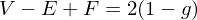
Magic Number: 2 times as many faces as vertices









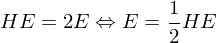
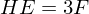
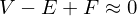
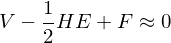
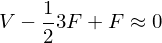
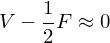
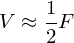
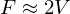
Magic Number: Average vertex valence is 6








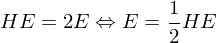
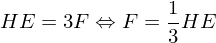
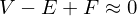
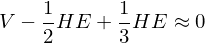
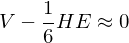
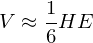
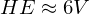
Magic Number: 5 platonic solids
A platonic solids with Schläfli symbol 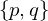is a polygonal mesh fulfilling the following properties:

• 
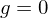
• All faces are -gons: 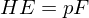(where )
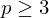• All vertices have valenc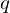e :   (where )

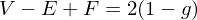
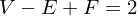
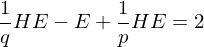
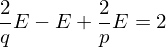
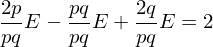
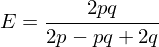
Number of edges cannot be negative:

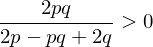
Since 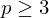and :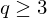


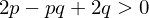
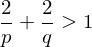
Gives only 5 solutions for :

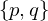• : Tetrahedron (4 triangular faces, self-dual)
• : Octahedron (8 triangular faces, dual to Cube)
• : Cube (6 square faces, dual to Octahedron)
• : Icosahedron (20 triangular faces, dual to Dodecahedron)
• : Dodecahedron (12 pentagonal faces, dual to Icosahedron)