This flashcard is just one of a free flashcard set. See all flashcards!
45
Was versteht man unter der notwendigen Bedingung für innere Extremstellen.
Bei einer inneren Extremstelle muss die erste Ableitung den Wert null besitzten, denn bei jeder inneren Extremstelle muss das Schaubild eine waagerechte Tangente besitzten.
Allerdings reicht es nicht umgekehrt nicht aus, zur Bestimmung der Extremstellen nur die Nullstellen der Ableitungsfunktion zu betrachten. (Diese sind nur "Kandidaten für Extremstellen".) Es gibt ja noch die Sattel- oder Terassenpunkte.
Aus einer inneren Extremstelle darf man auf die Nullstelle der Ableitungsfunktion schließen, nicht aber umkehrt.
Wir sagen: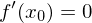 ist notwendig für eine Extremstelle, nicht aber hinreichend.
ist notwendig für eine Extremstelle, nicht aber hinreichend.
Allerdings reicht es nicht umgekehrt nicht aus, zur Bestimmung der Extremstellen nur die Nullstellen der Ableitungsfunktion zu betrachten. (Diese sind nur "Kandidaten für Extremstellen".) Es gibt ja noch die Sattel- oder Terassenpunkte.
Aus einer inneren Extremstelle darf man auf die Nullstelle der Ableitungsfunktion schließen, nicht aber umkehrt.
Wir sagen:
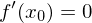 ist notwendig für eine Extremstelle, nicht aber hinreichend.
ist notwendig für eine Extremstelle, nicht aber hinreichend.Tags: Extremstelle, hinreichend, notwendig, Sattelpunkt, Terassenpunkt
Source:
Source:
Flashcard info:
Author: www.mathematik-bw.de
Main topic: Mathematik
Topic: 10. Klasse
School / Univ.: Clara-Schumann-Gymnasium
City: Lahr
Published: 23.12.2009

