Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
64
Beweis: MPKP 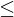 PKP II
PKP II 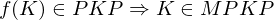
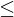 PKP II
PKP II 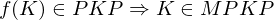
Sei 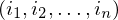 eine PKP Lösung minimaler Länge für f(K).
eine PKP Lösung minimaler Länge für f(K).
1.) Die Lösung beginnt und endet mit Anfangsstein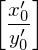 bzw. Schlussstein
bzw. Schlussstein 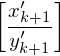 weil nur diese mit demselben Zeichen beginnen/enden
weil nur diese mit demselben Zeichen beginnen/enden
2.) Der Anfangsstein kann nicht in der Mitte vorkommen, da sonst im oberen Wort zwei # aufeinanderfolgen würden, was im unteren unmöglich ist.
3.) Der Schlussstein ist der letzte Stein, da sonst $ vorher auftreten würde und wir die korrespondierende Folge nach dem ersten Vorkommen des $-Zeichen abschneiden könnten und damit eine kürzere gefunden hätten.
Die PKP-Lösung von f(K) hat also die Struktur:
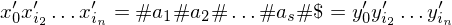
Daraus ergibt sich folgende MPKP-Lösung für K:
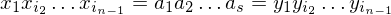
Es gilt also: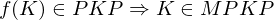
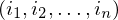 eine PKP Lösung minimaler Länge für f(K).
eine PKP Lösung minimaler Länge für f(K).1.) Die Lösung beginnt und endet mit Anfangsstein
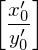 bzw. Schlussstein
bzw. Schlussstein 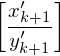 weil nur diese mit demselben Zeichen beginnen/enden
weil nur diese mit demselben Zeichen beginnen/enden2.) Der Anfangsstein kann nicht in der Mitte vorkommen, da sonst im oberen Wort zwei # aufeinanderfolgen würden, was im unteren unmöglich ist.
3.) Der Schlussstein ist der letzte Stein, da sonst $ vorher auftreten würde und wir die korrespondierende Folge nach dem ersten Vorkommen des $-Zeichen abschneiden könnten und damit eine kürzere gefunden hätten.
Die PKP-Lösung von f(K) hat also die Struktur:
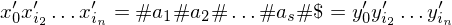
Daraus ergibt sich folgende MPKP-Lösung für K:
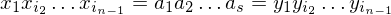
Es gilt also: