Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
58
Was ist die Walsh-Hadamard-Transformation ... wie erhält man die Basisvektoren?
(Merkmale)
(Merkmale)
Die Basisvektoren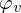 
erhält man aus den Walsh-Funktionen in dem man das Intervall (-0.5,+0.5) mit 
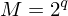Werten abtasten, wobei es nur Abtastwerte +/- 1 (Amplitude) gibt. Die Transformationsmatrix 
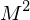lässt sich rekursiv aus der HADAMARD-Matrix mittels Kronecker-Produkt 
berechnen.
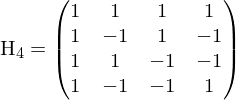
Diese Matrix enthält die Abtastwerte der ersten vier Walsh-Funktionen und bildet ein orthogonales Basensystem (alle Zeilen und Spalten orthogonal, nur 1 und -1 als Koeffizienten).
Die Hadamard-geordnete Walsh-Hadamard-Transformation (WHT) eines Mustervektors f mit M Komponenten erfolgt gemäß
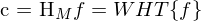
Die Inverse
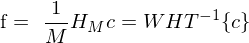
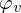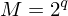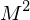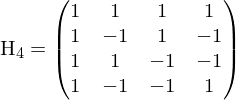
erhält man aus den Walsh-Funktionen in dem man das Intervall (-0.5,+0.5) mit Werten abtasten, wobei es nur Abtastwerte +/- 1 (Amplitude) gibt. Die Transformationsmatrix lässt sich rekursiv aus der HADAMARD-Matrix mittels Kronecker-Produkt berechnen.Diese Matrix enthält die Abtastwerte der ersten vier Walsh-Funktionen und bildet ein orthogonales Basensystem (alle Zeilen und Spalten orthogonal, nur 1 und -1 als Koeffizienten).
Die Hadamard-geordnete Walsh-Hadamard-Transformation (WHT) eines Mustervektors f mit M Komponenten erfolgt gemäß
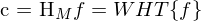
Die Inverse
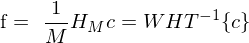
- nur Addition und Subtraktion nötig
- Resultat (c) sind reelle Zahlen
- gibt schnelle Implementierung mittels Faktorisierung
Karteninfo:
Autor: JanBo
Oberthema: Digitale Bildverarbeitung
Thema: Mustererkennung
Schule / Uni: Universität Koblenz-Landau
Ort: Koblenz
Veröffentlicht: 13.09.2012