Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
2
C7 ... (LK) bestimmte Integrale mit den Verfahren der partitiellen Integration, der Substitutionsmethode und der Partitialbruchzerlegung berechnen.
Partitielle Integration
Für die partitielle Integration gilt :
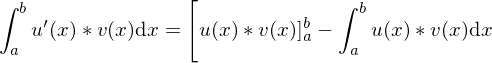
Substitutionsmethode
Gesucht sei die Stammfunktion von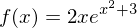 .
.
Also
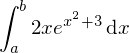
Dann ersetzen wir im Exponenten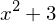 durch z
durch z
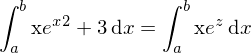
Anschließend formen wir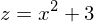 nach x um.
nach x um.
Jetzt können wir auch das x ersetzen.
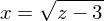
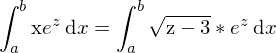
Jetzt müssen wir noch dx durch dz ersetzen.
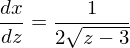
Nach Multiplikation mit dz erhalten wir
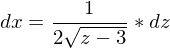
und können dx durch die ermittelte Funktion ersetzen
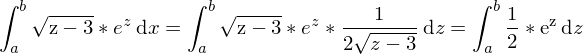
Dies lässt sich schon einfacher integrieren
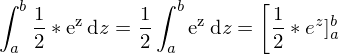
Nun müssen wir rücksubtitionieren
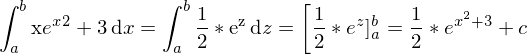
Beispiel Substitution
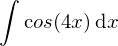
Substitution :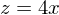
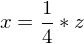
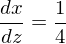
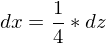
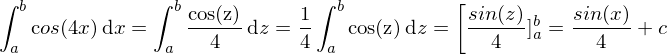
Partitialbruchzerlegung
Ermittelt werden soll die Stammfunktion von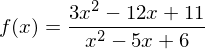
Also
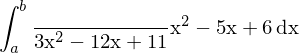
Zählergrad gleich Nennergrad oder größer, als erstes Polynomdivision
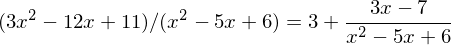
Daraus folgt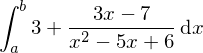
Zählergrad kleiner Nennergrad -> besitzt der Nenner Nullstellen
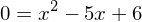 ->
-> 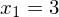 und
und 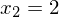
->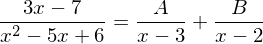
Den Term multiplizieren wir mit dem Hauptnenner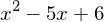
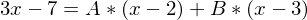
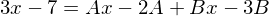
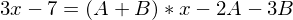
->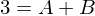 und
und 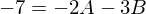
Nach lösen der zwei ermittelten Gleichungen ergeben sich für A und B folgende Werte:
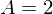 und
und 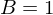
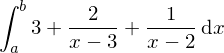
Nun kann man einfach die Stammfunktion ermitteln
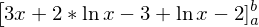
Für die partitielle Integration gilt :
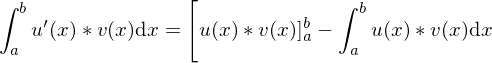
Substitutionsmethode
Gesucht sei die Stammfunktion von
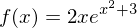 .
.Also
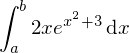
Dann ersetzen wir im Exponenten
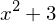 durch z
durch z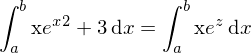
Anschließend formen wir
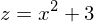 nach x um.
nach x um.Jetzt können wir auch das x ersetzen.
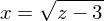
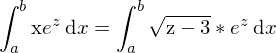
Jetzt müssen wir noch dx durch dz ersetzen.
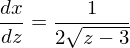
Nach Multiplikation mit dz erhalten wir
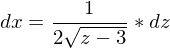
und können dx durch die ermittelte Funktion ersetzen
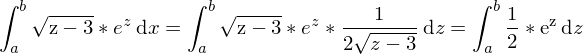
Dies lässt sich schon einfacher integrieren
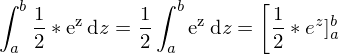
Nun müssen wir rücksubtitionieren
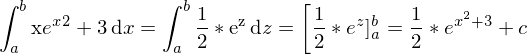
Beispiel Substitution
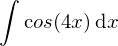
Substitution :
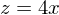
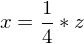
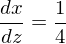
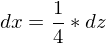
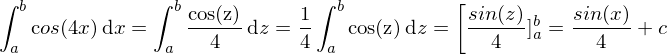
Partitialbruchzerlegung
Ermittelt werden soll die Stammfunktion von
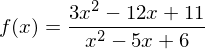
Also
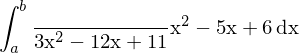
Zählergrad gleich Nennergrad oder größer, als erstes Polynomdivision
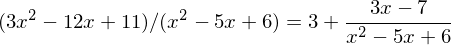
Daraus folgt
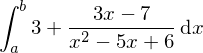
Zählergrad kleiner Nennergrad -> besitzt der Nenner Nullstellen
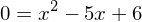 ->
-> 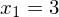 und
und 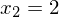
->
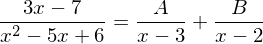
Den Term multiplizieren wir mit dem Hauptnenner
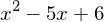
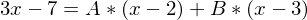
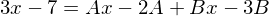
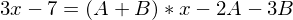
->
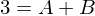 und
und 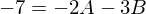
Nach lösen der zwei ermittelten Gleichungen ergeben sich für A und B folgende Werte:
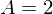 und
und 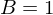
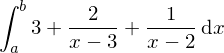
Nun kann man einfach die Stammfunktion ermitteln
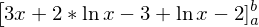
Tags:
Quelle: Alexander Barth
Quelle: Alexander Barth
Karteninfo:
Autor: Exinator
Oberthema: Mathematik
Thema: Abiturvorbereitung
Schule / Uni: MGS
Ort: Schwelm
Veröffentlicht: 28.03.2011

