This flashcard is just one of a free flashcard set. See all flashcards!
37
Explain Surface-Based Hole Filling! What are some problems of this approach?
Input: Boundary loop consisting of vertices 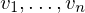 .
.
Goal: Triangulation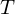 of the loop interior which minimizes some triangulation cost
of the loop interior which minimizes some triangulation cost 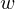 which is a combination of e.g.
which is a combination of e.g.
which produces a hole filling with low area and low normal deviation.
We denote by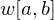 the cost of the best triangulation for only the vertices
the cost of the best triangulation for only the vertices 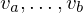 .
.
Obviously:
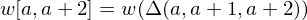
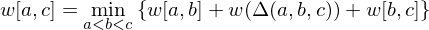
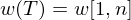
Solve using dynamic programming.
Complexity: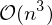 (Compute table for
(Compute table for 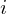 and
and 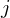 . For every entry, consider
. For every entry, consider 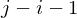 possible middle triangles)
possible middle triangles)
Optional post-processing steps
Refine the triangulation of the hole.
Apply smoothing to the hole region.
Problems
Does not work for islands.
Does not consider self-intersections.
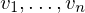 .
.Goal: Triangulation
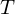 of the loop interior which minimizes some triangulation cost
of the loop interior which minimizes some triangulation cost 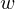 which is a combination of e.g.
which is a combination of e.g.- the area of the triangles
- the maximum dihedral angle
which produces a hole filling with low area and low normal deviation.
We denote by
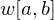 the cost of the best triangulation for only the vertices
the cost of the best triangulation for only the vertices 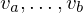 .
.Obviously:
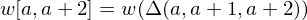
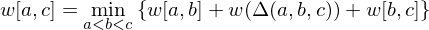
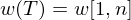
Solve using dynamic programming.
Complexity:
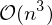 (Compute table for
(Compute table for 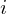 and
and 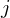 . For every entry, consider
. For every entry, consider 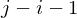 possible middle triangles)
possible middle triangles)Optional post-processing steps
Refine the triangulation of the hole.
Apply smoothing to the hole region.
Problems
Does not work for islands.
Does not consider self-intersections.
Flashcard info:
Author: janisborn
Main topic: Informatik
Topic: Computergrafik
School / Univ.: RWTH Aachen
City: Aachen
Published: 18.05.2022

