This flashcard is just one of a free flashcard set. See all flashcards!
11
Einheitswurzel
 Ring und
Ring und  natürliche Zahl mit
natürliche Zahl mit 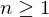 . Ein
. Ein 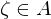 heißt
heißt  -te Einheitswurzel, falls eine der folgenden äquivalten Bedingungen erfüllt sind:
-te Einheitswurzel, falls eine der folgenden äquivalten Bedingungen erfüllt sind:(a)
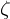 ist Nullstelle des Polynoms
ist Nullstelle des Polynoms 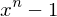
(b) Es ist
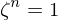
- ist
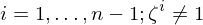 , so heißt
, so heißt 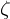 primitiv.
primitiv.-
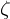 ist Element der Einheitengruppe, insbesondere bilden alle
ist Element der Einheitengruppe, insbesondere bilden alle  -ten Einheitswurzeln eine Untergruppe der Einheitengruppe.
-ten Einheitswurzeln eine Untergruppe der Einheitengruppe.
