This flashcard is just one of a free flashcard set. See all flashcards!
18
Simulation einer k-Band TM M als 1-Band TM M'
Eine k-Band TM M mit Rechenzeit t(n) und Platz s(n), kann von einer 1-Band TM M' mit Zeitbedarf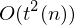 
und Platzbedarf O(s(n)) simuliert werden.
M' verwendet 2k Spuren:
- ungerade Spuren 1,3,...2k-1 enthalten den Inhalt der Bänder 1...k von M
- gerade Spuren 2,4,...,2k enthalten die Kopfpostitionen von M (mit # markiert)
Die Initialisierung der Spuren ist in konstanter Zeit möglich
Jeder Rechenschritt wird wie folgt simuliert:
- M' geht vom linkesten # bis zum rechtesten # (M' kennt Zustand von M)
- k Zeichen an mit # markierten Positionen werden im Zustandsraum gespeichert (möglich, da nur konstant viele Markierungen)
- M' wertet Übergangsfunktion von M aus (kennt nun neuen Zustand und Bandbewegungen)
- M' läuft zum linkesten # zurück und verändert Bandinschriften und verschiebt # nach links oder rechts.
Laufzeit: Nach t Schritten können die äußeren Markierungen höchstens 2t Positionen auseinander liegen (pro Schritt nur um eine Position verschoben) => Abstand zwischen Zeichen durch O(t(n)) beschränkt => Laufzeit pro Schritt durch O(t(n)) beschränkt => Simulation von t(n) Schritten durch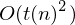
beschränkt
Platzbedarf:linear (zu jeder von M' besuchten Zelle gehört mind. eine Zelle, die M besucht?)
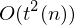und Platzbedarf O(s(n)) simuliert werden.M' verwendet 2k Spuren:
- ungerade Spuren 1,3,...2k-1 enthalten den Inhalt der Bänder 1...k von M
- gerade Spuren 2,4,...,2k enthalten die Kopfpostitionen von M (mit # markiert)
Die Initialisierung der Spuren ist in konstanter Zeit möglich
Jeder Rechenschritt wird wie folgt simuliert:
- M' geht vom linkesten # bis zum rechtesten # (M' kennt Zustand von M)
- k Zeichen an mit # markierten Positionen werden im Zustandsraum gespeichert (möglich, da nur konstant viele Markierungen)
- M' wertet Übergangsfunktion von M aus (kennt nun neuen Zustand und Bandbewegungen)
- M' läuft zum linkesten # zurück und verändert Bandinschriften und verschiebt # nach links oder rechts.
Laufzeit: Nach t Schritten können die äußeren Markierungen höchstens 2t Positionen auseinander liegen (pro Schritt nur um eine Position verschoben) => Abstand zwischen Zeichen durch O(t(n)) beschränkt => Laufzeit pro Schritt durch O(t(n)) beschränkt => Simulation von t(n) Schritten durch
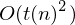beschränktPlatzbedarf:linear (zu jeder von M' besuchten Zelle gehört mind. eine Zelle, die M besucht?)
