This flashcard is just one of a free flashcard set. See all flashcards!
33
Bei einer Funktion f gilt für alle 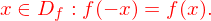
Was bedeutet dies für das zugehörige Schaubild?
Nenne drei unterschiedliche Funktionstypen mit dieser Eigenschaft in der allgemeinen Form.
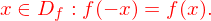
Was bedeutet dies für das zugehörige Schaubild?
Nenne drei unterschiedliche Funktionstypen mit dieser Eigenschaft in der allgemeinen Form.
Aus der Bedingung folgt die (Achsen-)Symmetrie des Schaubildes von f zur y-Achse
Beachte, dass man die entsprechende Funktion als "gerade" bezeichnet - nicht aber das Schaubild!
Beispiele:
- Jede konstante Funktion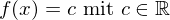
- Potenzfunktionen mit gerader, ganzzahligen Hochzahl:
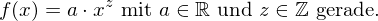
- Jede ganzrationale Funktion mit ausschließlich geraden
"x-Potenzen" .
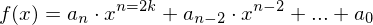
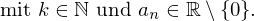
- Die Kosinusfunktion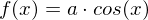 mit beliebigem
mit beliebigem
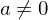 .
.
- Die Nullfunktion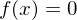 . (Einzige Funktion die sowohl
. (Einzige Funktion die sowohl
gerade, als auch ungerade ist.)
Bemerkungen:
In Worten bedeutet die obige Gleichung: "Betrachtet man
auf der x-Achse eine Zahl und ihre Gegenzahl, so sind auch die entsprechenden y-Werte identisch."
Gerade Zahlen haben immer die Form eines Produkt aus einer natürlichen Zahl mit 2.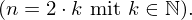
Beachte, dass man die entsprechende Funktion als "gerade" bezeichnet - nicht aber das Schaubild!
Beispiele:
- Jede konstante Funktion
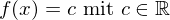
- Potenzfunktionen mit gerader, ganzzahligen Hochzahl:
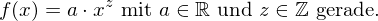
- Jede ganzrationale Funktion mit ausschließlich geraden
"x-Potenzen" .
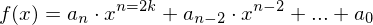
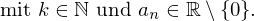
- Die Kosinusfunktion
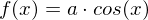 mit beliebigem
mit beliebigem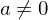 .
.- Die Nullfunktion
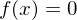 . (Einzige Funktion die sowohl
. (Einzige Funktion die sowohlgerade, als auch ungerade ist.)
Bemerkungen:
In Worten bedeutet die obige Gleichung: "Betrachtet man
auf der x-Achse eine Zahl und ihre Gegenzahl, so sind auch die entsprechenden y-Werte identisch."
Gerade Zahlen haben immer die Form eines Produkt aus einer natürlichen Zahl mit 2.
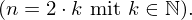
Tags: Begriffe, Funktion, ganzrational, Symmetrie
Source:
Source:
Flashcard info:
Author: www.mathematik-bw.de
Main topic: Mathematik
Topic: 10. Klasse
School / Univ.: Clara-Schumann-Gymnasium
City: Lahr
Published: 23.12.2009

