This flashcard is just one of a free flashcard set. See all flashcards!
12
Wie erreiche ich die Unabhängigkeit von ungewollten Eigenschaften der Features?
Die Berechnung eines Haar-Integrals auf einer Feature-Extraktionsfunktion  ermöglicht die Konstruktion einer Feature-Extraktionsfunktion
ermöglicht die Konstruktion einer Feature-Extraktionsfunktion  , die invariant bezüglich einer parametrisierbaren Transformationsfunktion
, die invariant bezüglich einer parametrisierbaren Transformationsfunktion 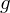 ist. Um eine Invarianz von
ist. Um eine Invarianz von  zu erreichen, wird der Durchschnitt der extrahierten Feature-Werte über den Anwendungen aller möglichen Transformationsfunktionen berechnet. Das Haar-Integra wird definiert wie folgt:
zu erreichen, wird der Durchschnitt der extrahierten Feature-Werte über den Anwendungen aller möglichen Transformationsfunktionen berechnet. Das Haar-Integra wird definiert wie folgt:

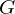 ist dabei die Menge aller Transformationsfunktionen, die durch unterschiedliche Parametrisierungen von
ist dabei die Menge aller Transformationsfunktionen, die durch unterschiedliche Parametrisierungen von 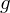 erreicht werden kann. Für den Praxis-Einsatz sind Integrale eher hinderlich. Da unsere Objekte im diskreten Raum liegen und G eine endliche Menge ist, kann das Haar-Integral so geschrieben werden:
erreicht werden kann. Für den Praxis-Einsatz sind Integrale eher hinderlich. Da unsere Objekte im diskreten Raum liegen und G eine endliche Menge ist, kann das Haar-Integral so geschrieben werden:

 ermöglicht die Konstruktion einer Feature-Extraktionsfunktion
ermöglicht die Konstruktion einer Feature-Extraktionsfunktion  , die invariant bezüglich einer parametrisierbaren Transformationsfunktion
, die invariant bezüglich einer parametrisierbaren Transformationsfunktion 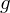 ist. Um eine Invarianz von
ist. Um eine Invarianz von  zu erreichen, wird der Durchschnitt der extrahierten Feature-Werte über den Anwendungen aller möglichen Transformationsfunktionen berechnet. Das Haar-Integra wird definiert wie folgt:
zu erreichen, wird der Durchschnitt der extrahierten Feature-Werte über den Anwendungen aller möglichen Transformationsfunktionen berechnet. Das Haar-Integra wird definiert wie folgt:
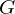 ist dabei die Menge aller Transformationsfunktionen, die durch unterschiedliche Parametrisierungen von
ist dabei die Menge aller Transformationsfunktionen, die durch unterschiedliche Parametrisierungen von 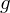 erreicht werden kann. Für den Praxis-Einsatz sind Integrale eher hinderlich. Da unsere Objekte im diskreten Raum liegen und G eine endliche Menge ist, kann das Haar-Integral so geschrieben werden:
erreicht werden kann. Für den Praxis-Einsatz sind Integrale eher hinderlich. Da unsere Objekte im diskreten Raum liegen und G eine endliche Menge ist, kann das Haar-Integral so geschrieben werden:
Tags:
Source: MMDB 2009 Kapitel 5
Source: MMDB 2009 Kapitel 5
Flashcard info:
Author: kread
Main topic: Informatik
Topic: Semantic Web
School / Univ.: Universität Koblenz-Landau
City: Koblenz
Published: 22.10.2010

