Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
44
semi-entscheidbar/rekursiv aufzählbar
Eine Sprache L ist genau dann semi-entscheidbar, wenn L rekursiv aufzählbar ist
Beweis:
"<=": Konstruiere aus einem Auzähler für L eine TM M, die L erkennt
- zusätzliche Spur, die Rolle des Drucker übernimmt
- wenn neues Wort enummeriert wurde, vergleicht es M mit w
- falls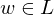 wird w irgendwann enummeriert und von M akzeptiert
wird w irgendwann enummeriert und von M akzeptiert
- falls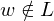 wird w nicht akzeptiert, aber M hält auch nicht
wird w nicht akzeptiert, aber M hält auch nicht
"=>": Konstruiere aus eine TM M, die L erkennt einen Aufzähler
- führe i Schritte von M auf Wörtern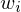 aus (kanonische Reihenfolge)
aus (kanonische Reihenfolge)
- wird ein Wort akzeptiert, drucke es aus
- falls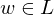 wird L nach endlich vielen Schritten gedruckt
wird L nach endlich vielen Schritten gedruckt
- falls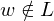 wird w nie gedruckt
wird w nie gedruckt
Beweis:
"<=": Konstruiere aus einem Auzähler für L eine TM M, die L erkennt
- zusätzliche Spur, die Rolle des Drucker übernimmt
- wenn neues Wort enummeriert wurde, vergleicht es M mit w
- falls
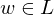 wird w irgendwann enummeriert und von M akzeptiert
wird w irgendwann enummeriert und von M akzeptiert- falls
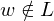 wird w nicht akzeptiert, aber M hält auch nicht
wird w nicht akzeptiert, aber M hält auch nicht"=>": Konstruiere aus eine TM M, die L erkennt einen Aufzähler
- führe i Schritte von M auf Wörtern
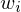 aus (kanonische Reihenfolge)
aus (kanonische Reihenfolge)- wird ein Wort akzeptiert, drucke es aus
- falls
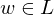 wird L nach endlich vielen Schritten gedruckt
wird L nach endlich vielen Schritten gedruckt- falls
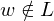 wird w nie gedruckt
wird w nie gedruckt 
