Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
41
Explain the Incremental Delaunay algorithm!
Start with one triangle that is large enough to contain all input points.
Invariant: The current triangulation is Delaunay.
Repeat: Pick next input vertex. Find triangle into which input vertex falls and split into three new triangles (1:3 split). Now, the newly inserted triangles might have lost their Delaunay property. Mark the edges of the triangle into which the current vertex was inserted.
For each marked edge, check the local Delaunay properties of the two incident triangles. If it is violated, flip the edge and mark the edges around the current quad configuration.
Complexity
We examine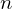 points:
points: 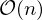
For each point, we find in which triangle it falls. Using a search tree: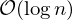
After each insertion, we flip some edges. It can be shown, that the number of flipped edges per insertion is constant on average: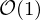
Thus, the Incremental Delaunay algorithm has a complexity of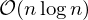 .
.
Invariant: The current triangulation is Delaunay.
Repeat: Pick next input vertex. Find triangle into which input vertex falls and split into three new triangles (1:3 split). Now, the newly inserted triangles might have lost their Delaunay property. Mark the edges of the triangle into which the current vertex was inserted.
For each marked edge, check the local Delaunay properties of the two incident triangles. If it is violated, flip the edge and mark the edges around the current quad configuration.
Complexity
We examine
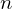 points:
points: 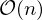
For each point, we find in which triangle it falls. Using a search tree:
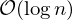
After each insertion, we flip some edges. It can be shown, that the number of flipped edges per insertion is constant on average:
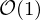
Thus, the Incremental Delaunay algorithm has a complexity of
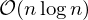 .
.Karteninfo:
Autor: janisborn
Oberthema: Informatik
Thema: Computergrafik
Schule / Uni: RWTH Aachen
Ort: Aachen
Veröffentlicht: 18.05.2022

