Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
43
Wie kann man die Covarianz-Matrix interpretieren?
Die Kovarianz-Matrix (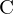
) ist eine quadratische Matrix mit Dim 
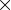Dim Einträgen (Dim = Anzahl der Merkmale/Features/Variablen). Sie enthält alle Kovarianzen zwischen allen Dimensionen.
$ C = \begin{pmatrix} cov(x,x) & cov(x,y) \\ cov(y,x) & cov(y,y) \end{pmatrix} $
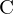) ist eine quadratische Matrix mit Dim 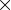Dim Einträgen (Dim = Anzahl der Merkmale/Features/Variablen). Sie enthält alle Kovarianzen zwischen allen Dimensionen. $ C = \begin{pmatrix} cov(x,x) & cov(x,y) \\ cov(y,x) & cov(y,y) \end{pmatrix} $
Karteninfo:
Autor: JanBo
Oberthema: Digitale Bildverarbeitung
Thema: IPCV
Schule / Uni: Universität Koblenz-Landau
Ort: Koblenz
Veröffentlicht: 20.11.2010