Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
24
B7: Graphenuntersuchung auf Krümmungsverhalten, Wende- und Sattelstellen
1) Krümmungsverhalten:
Wenn f''(x)>0 {f''(x)<0} gilt, dann ist der Graph von f linksgerümmt {rechtsgekrümmt}. Der Graf vom f heißt linksgekrümmt {rechtsgekrümmt } genau dann, wenn f' streng monoton steigend {fallend} ist.
2) Wendepunkte:
Notwendige Bedingung:
f''(xo)=0
Hinreichende Bedingung:
f'''(xo)>0 R/L Wendestelle
f'''(xo)<0 L/R Wendestelle
3) Sattelpunkte:
Sattelpunkte sind Wendepunkte, mit einer zur x-Achse parallelen Tangente
Wenn gilt:
f'(xo)=0
f''(xo)=0
sowie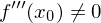 -> nur, wenn das gilt, gibt es einen Sattelpunkt.
-> nur, wenn das gilt, gibt es einen Sattelpunkt.
Wenn f''(x)>0 {f''(x)<0} gilt, dann ist der Graph von f linksgerümmt {rechtsgekrümmt}. Der Graf vom f heißt linksgekrümmt {rechtsgekrümmt } genau dann, wenn f' streng monoton steigend {fallend} ist.
2) Wendepunkte:
Notwendige Bedingung:
f''(xo)=0
Hinreichende Bedingung:
f'''(xo)>0 R/L Wendestelle
f'''(xo)<0 L/R Wendestelle
3) Sattelpunkte:
Sattelpunkte sind Wendepunkte, mit einer zur x-Achse parallelen Tangente
Wenn gilt:
f'(xo)=0
f''(xo)=0
sowie
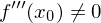 -> nur, wenn das gilt, gibt es einen Sattelpunkt.
-> nur, wenn das gilt, gibt es einen Sattelpunkt.Karteninfo:
Autor: Exinator
Oberthema: Mathematik
Thema: Abiturvorbereitung
Schule / Uni: MGS
Ort: Schwelm
Veröffentlicht: 28.03.2011

