This flashcard is just one of a free flashcard set. See all flashcards!
114
Draw a unit cube using 1-Point / 2-Point / 3-Point Perspective!
1-Point:
Vanishing point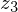 is identical with the projection center
is identical with the projection center 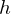 . Draw lines from cube edge
. Draw lines from cube edge 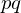 to
to 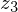 . The vanishing points of the cube diagonals
. The vanishing points of the cube diagonals  are found by adding lines with distance
are found by adding lines with distance 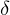 to the projection center, parallel to the edges of the cube.
to the projection center, parallel to the edges of the cube.
2-Point:
Vanishing points ,
, 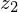 lie on a line with the projection center
lie on a line with the projection center 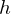 . Given a cube edge
. Given a cube edge 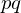 , add connections from the end vertices to the vanishing points.
, add connections from the end vertices to the vanishing points.
Now, consider shifting the upper corner of the cube into the projection center. Then,
of the cube into the projection center. Then,  forms a right triangle with
forms a right triangle with  and
and 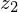 , where
, where 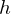 is the footpoint of
is the footpoint of  . Given the lengths
. Given the lengths 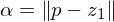 ,
, 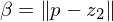 , we can construct the vanishing points of the diagonals of the cube.
, we can construct the vanishing points of the diagonals of the cube.
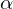 and
and 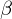 can be found geometrically by constructing a half circle above
can be found geometrically by constructing a half circle above 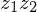 and intersecting it with the perpendicular above
and intersecting it with the perpendicular above 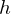 .
.
3-Point:
Only the three vanishing points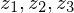 are given. The projection center
are given. The projection center 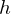 is found by intersecting the three heights of the triangle
is found by intersecting the three heights of the triangle 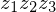 . Based on these heights, we again use Thales' theorem to find the right triangles above the edges of the vanishing point triangle. By intersecting the angle bisectors with the respective edges, the diagonal vanishing points
. Based on these heights, we again use Thales' theorem to find the right triangles above the edges of the vanishing point triangle. By intersecting the angle bisectors with the respective edges, the diagonal vanishing points 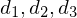 are found.
are found.
Vanishing point
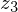 is identical with the projection center
is identical with the projection center 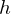 . Draw lines from cube edge
. Draw lines from cube edge 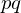 to
to 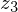 . The vanishing points of the cube diagonals
. The vanishing points of the cube diagonals  are found by adding lines with distance
are found by adding lines with distance 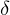 to the projection center, parallel to the edges of the cube.
to the projection center, parallel to the edges of the cube.2-Point:
Vanishing points
 ,
, 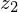 lie on a line with the projection center
lie on a line with the projection center 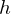 . Given a cube edge
. Given a cube edge 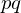 , add connections from the end vertices to the vanishing points.
, add connections from the end vertices to the vanishing points.Now, consider shifting the upper corner
 of the cube into the projection center. Then,
of the cube into the projection center. Then,  forms a right triangle with
forms a right triangle with  and
and 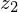 , where
, where 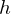 is the footpoint of
is the footpoint of  . Given the lengths
. Given the lengths 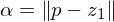 ,
, 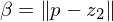 , we can construct the vanishing points of the diagonals of the cube.
, we can construct the vanishing points of the diagonals of the cube.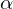 and
and 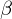 can be found geometrically by constructing a half circle above
can be found geometrically by constructing a half circle above 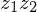 and intersecting it with the perpendicular above
and intersecting it with the perpendicular above 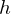 .
.3-Point:
Only the three vanishing points
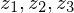 are given. The projection center
are given. The projection center 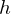 is found by intersecting the three heights of the triangle
is found by intersecting the three heights of the triangle 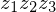 . Based on these heights, we again use Thales' theorem to find the right triangles above the edges of the vanishing point triangle. By intersecting the angle bisectors with the respective edges, the diagonal vanishing points
. Based on these heights, we again use Thales' theorem to find the right triangles above the edges of the vanishing point triangle. By intersecting the angle bisectors with the respective edges, the diagonal vanishing points 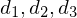 are found.
are found.Flashcard info:
Author: janisborn
Main topic: Informatik
Topic: Computergrafik
School / Univ.: RWTH Aachen
City: Aachen
Published: 18.05.2022

