Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
8
D1: Definitionslücken bestimmen und feststellen, ob diese behebbar sind oder nicht, und im zweiten Fall die Gleichung der zugehörigen senkrechten Asymptote angeben.
Bestimmung von Definitionslücken:
Eine gebrochenrationale Funktion f ist der Quotient aus zwei ganzrationalen Funktionen z und n. Es gilt also:
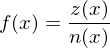Da die Teilbarkeit durch 0 auszuschließen ist, ist der Definitionsbereich gebrochenrationaler Funktionen durch die Nullstellen des Nennerpolynoms eingeschränkt. Hat das Nennerpolynom keine Nullstellen so ist D=R.
Zur Bestimmung der Nullstellen sollten zuerst Nenner und Zähler soweit wie möglich faktorisiert werden. Dazu dienen das Ausklammern, Binomische Formeln sowie die Polynomdivision.
Eine gebrochenrationale Funktion f ist der Quotient aus zwei ganzrationalen Funktionen z und n. Es gilt also:
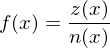Da die Teilbarkeit durch 0 auszuschließen ist, ist der Definitionsbereich gebrochenrationaler Funktionen durch die Nullstellen des Nennerpolynoms eingeschränkt. Hat das Nennerpolynom keine Nullstellen so ist D=R.Zur Bestimmung der Nullstellen sollten zuerst Nenner und Zähler soweit wie möglich faktorisiert werden. Dazu dienen das Ausklammern, Binomische Formeln sowie die Polynomdivision.
Karteninfo:
Autor: Exinator
Oberthema: Mathematik
Thema: Abiturvorbereitung
Schule / Uni: MGS
Ort: Schwelm
Veröffentlicht: 28.03.2011