This flashcard is just one of a free flashcard set. See all flashcards!
29
Wie lauten die Gleichungen der Tangenen und der Normalen an die Normalparabel an der Stelle x=1,5?
Zugehörige Funktion: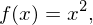 
Tangentensteigung aus Ableitungsfunktion 
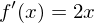somit beträgt die Tangentsteigung an der Stelle 1,5: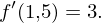 
Der y-Wert an der Stelle 1,5 ist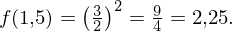
Verschiebt man eine Ursprungsgerade mit der Steigung 3 um 1,5 in x-Richtung und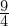
in y-Richtung erhält man die gesuchte Tangente. Ihre Gleichung lautet:
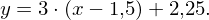
Aufgrund der Orthogonalitätsbedingung folgt für die Gleichung der zugehörigen Normalen:
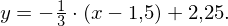
Hinweis:
In der Hauptform (mit Steigung und y-Achsenabschnitt) lauten die Gleichungen:
Tangente: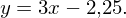
Normale: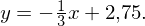
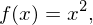Tangentensteigung aus Ableitungsfunktion 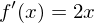somit beträgt die Tangentsteigung an der Stelle 1,5: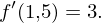 Der y-Wert an der Stelle 1,5 ist
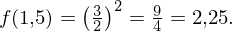
Verschiebt man eine Ursprungsgerade mit der Steigung 3 um 1,5 in x-Richtung und
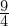in y-Richtung erhält man die gesuchte Tangente. Ihre Gleichung lautet: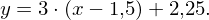 Aufgrund der Orthogonalitätsbedingung folgt für die Gleichung der zugehörigen Normalen:
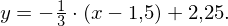
Hinweis:
In der Hauptform (mit Steigung und y-Achsenabschnitt) lauten die Gleichungen:
Tangente:
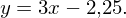
Normale:
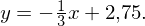
Tags: Gerade, Normale, Tangente, Verschiebung
Source:
Source:
Flashcard info:
Author: www.mathematik-bw.de
Main topic: Mathematik
Topic: 10. Klasse
School / Univ.: Clara-Schumann-Gymnasium
City: Lahr
Published: 23.12.2009