This flashcard is just one of a free flashcard set. See all flashcards!
31
Erkläre die Primfaktorzerlegung
Sei n eine natürliche Zahl mit n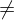
0.
Ein Produkt von Primzahlen p_1 \cdot p_2 \cdot ... \cdot p_m = n heißt Primfaktorzerlegung von n.
Jede Zahl n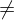0 besitzt eine solche Primfaktorzerlegung.
Wenn man zudem verlangt, dass die Primzahlen in aufsteigender Reihenfolge angeordnet sind, dann ist die Primfaktorzerlegung einer Zahl eindeutig.
Bsp: 55=5*11
Achtung: Die Primfaktorzerlegung von 1 ist das leere Produkt.
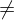0.Ein Produkt von Primzahlen p_1 \cdot p_2 \cdot ... \cdot p_m = n heißt Primfaktorzerlegung von n.
Jede Zahl n
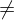0 besitzt eine solche Primfaktorzerlegung.Wenn man zudem verlangt, dass die Primzahlen in aufsteigender Reihenfolge angeordnet sind, dann ist die Primfaktorzerlegung einer Zahl eindeutig.
Bsp: 55=5*11
Achtung: Die Primfaktorzerlegung von 1 ist das leere Produkt.
Tags: VL vom 4.5.10
Source:
Source:
Flashcard info:
Author: P-H-I-L
Main topic: Mathematik
Topic: Mathematische Strukturen
Published: 13.04.2010