This flashcard is just one of a free flashcard set. See all flashcards!
52
Lemma Reduktion
Falls 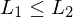 und
und 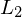 rekursiv (rekursiv aufzählbar) ist, so ist auch
rekursiv (rekursiv aufzählbar) ist, so ist auch 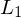 rekursiv (rekursiv aufzählbar).
rekursiv (rekursiv aufzählbar).
Beweis:

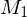 akz.
akz. 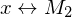 akz.
akz. 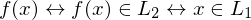
Falls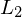 rekursiv ist, ist die Terminierung von
rekursiv ist, ist die Terminierung von 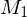 auf jeder Eingabe gesichert. Falls
auf jeder Eingabe gesichert. Falls 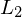 rek. aufz. ist, ist die Terminierung von
rek. aufz. ist, ist die Terminierung von 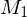 auf Eingaben aus
auf Eingaben aus 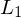 gesichert.
gesichert.
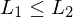 und
und 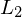 rekursiv (rekursiv aufzählbar) ist, so ist auch
rekursiv (rekursiv aufzählbar) ist, so ist auch 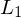 rekursiv (rekursiv aufzählbar).
rekursiv (rekursiv aufzählbar).Beweis:

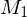 akz.
akz. 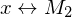 akz.
akz. 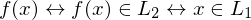
Falls
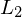 rekursiv ist, ist die Terminierung von
rekursiv ist, ist die Terminierung von 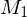 auf jeder Eingabe gesichert. Falls
auf jeder Eingabe gesichert. Falls 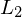 rek. aufz. ist, ist die Terminierung von
rek. aufz. ist, ist die Terminierung von 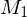 auf Eingaben aus
auf Eingaben aus 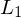 gesichert.
gesichert.
