This flashcard is just one of a free flashcard set. See all flashcards!
34
Beweis: Das Halteproblem ist nicht rekursiv
Zum Zweck des Widerspruchs nehmen wir an, dass H entscheidbar ist. Dann gib es eine TM  , die H entscheidet.
, die H entscheidet.
Konstruieren nun eine TM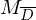 , die
, die  als Unterprgramm aufruft und
als Unterprgramm aufruft und 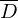 entscheidet.
entscheidet.
(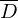 ist unentscheidbar, als kann es
ist unentscheidbar, als kann es  nicht geben)
nicht geben)
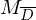 arbeitet wie folgt:
arbeitet wie folgt:
1.) Auf Eingabe w, berechne i, so dass gilt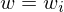
2.) Berechne nun Gödelnummer der i-ten TM: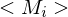
3.) Starte als Unterprogramm auf Eingabe
als Unterprogramm auf Eingabe 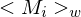
4.) Falls akzeptiert, simuliere
akzeptiert, simuliere 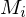 auf w und übernehme deren Akzeptanzverhalten
auf w und übernehme deren Akzeptanzverhalten
5.) Falls verwirft, so verwirf
verwirft, so verwirf
Korrektheit:
1.Fall: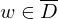 =>
=>  akzeptiert
akzeptiert 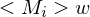 , da
, da 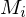 auf w hält=>
auf w hält=>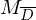 akzeptiert w
akzeptiert w
2.Fall: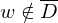 =>
=>  akzeptiert, falls
akzeptiert, falls 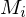 w verwirft oder
w verwirft oder  verwirft, falls
verwirft, falls 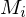 nicht hält (also weder verwirft noch akzeptiert)=>in beiden Fällen:
nicht hält (also weder verwirft noch akzeptiert)=>in beiden Fällen: 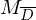 verwirft w.
verwirft w.
 , die H entscheidet.
, die H entscheidet.Konstruieren nun eine TM
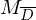 , die
, die  als Unterprgramm aufruft und
als Unterprgramm aufruft und 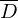 entscheidet.
entscheidet.(
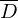 ist unentscheidbar, als kann es
ist unentscheidbar, als kann es  nicht geben)
nicht geben)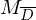 arbeitet wie folgt:
arbeitet wie folgt:1.) Auf Eingabe w, berechne i, so dass gilt
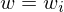
2.) Berechne nun Gödelnummer der i-ten TM:
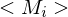
3.) Starte
 als Unterprogramm auf Eingabe
als Unterprogramm auf Eingabe 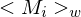
4.) Falls
 akzeptiert, simuliere
akzeptiert, simuliere 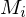 auf w und übernehme deren Akzeptanzverhalten
auf w und übernehme deren Akzeptanzverhalten5.) Falls
 verwirft, so verwirf
verwirft, so verwirfKorrektheit:
1.Fall:
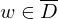 =>
=>  akzeptiert
akzeptiert 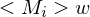 , da
, da 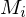 auf w hält=>
auf w hält=>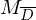 akzeptiert w
akzeptiert w2.Fall:
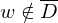 =>
=>  akzeptiert, falls
akzeptiert, falls 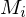 w verwirft oder
w verwirft oder  verwirft, falls
verwirft, falls 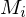 nicht hält (also weder verwirft noch akzeptiert)=>in beiden Fällen:
nicht hält (also weder verwirft noch akzeptiert)=>in beiden Fällen: 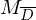 verwirft w.
verwirft w.
