This flashcard is just one of a free flashcard set. See all flashcards!
1
A3 ...die Gleichung einer Tangente und einer Normale an den Graphen einer Funktion in einem Punkt bestimmen
Funktion : f(x) = - x² - x + 2
Die Gleichungen von Tangente und Normale sollen für den Punkt
P (2/ f(2)) blestimmt werden.
Vorüberlegung
Die Tangente ist eine Gerade mit der Gleichung
.
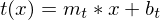Die Normale ist eine dazu senkrechte Gerade mit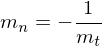
also mit der Gleichung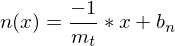 
Die Steigung der Tangenten entspricht der Steigung des Graphen von f(x) im Punkt P.
Rechnung
f(x) = - x² - x + 2 -> f'(x) = - 2x - 1
Koordinaten des Punktes P( 2 / f(2) ):
f(2) = -2² - 2 + 2 = - 4 - 2 +2 = -4 -> P( 2/ - 4)
Steigung in P( 2 / - 4)
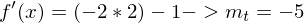(Tangentensteigung)
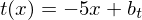
Die Tangente verläuft durch P(2 / - 4)
t(2) = - 4
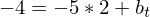
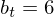
-> t(x) = - 5x + 6 ist die Tangente durch P ( 2 / - 4)
Normalengleichung
->
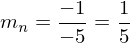
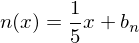
Die Normale verläuft durch den Punkt P( 2 / - 4 )
n(2) = - 4
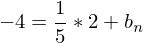
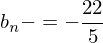
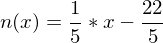
-> ist die Gleichung der Normalen die durch den Punkt P (2 / - 4) verläuft.
Die Gleichungen von Tangente und Normale sollen für den Punkt
P (2/ f(2)) blestimmt werden.
Vorüberlegung
Die Tangente ist eine Gerade mit der Gleichung
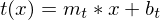.Die Normale ist eine dazu senkrechte Gerade mit
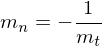also mit der Gleichung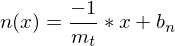 Die Steigung der Tangenten entspricht der Steigung des Graphen von f(x) im Punkt P.
Rechnung
f(x) = - x² - x + 2 -> f'(x) = - 2x - 1
Koordinaten des Punktes P( 2 / f(2) ):
f(2) = -2² - 2 + 2 = - 4 - 2 +2 = -4 -> P( 2/ - 4)
Steigung in P( 2 / - 4)
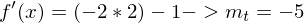(Tangentensteigung)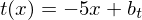 Die Tangente verläuft durch P(2 / - 4)
t(2) = - 4
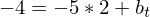
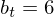
-> t(x) = - 5x + 6 ist die Tangente durch P ( 2 / - 4)
Normalengleichung
->
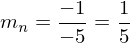
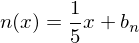
Die Normale verläuft durch den Punkt P( 2 / - 4 )
n(2) = - 4
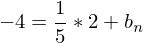
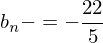
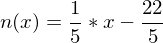
-> ist die Gleichung der Normalen die durch den Punkt P (2 / - 4) verläuft.
Tags:
Source: Alexander Barth
Source: Alexander Barth
Flashcard info:
Author: Exinator
Main topic: Mathematik
Topic: Abiturvorbereitung
School / Univ.: MGS
City: Schwelm
Published: 28.03.2011