Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
47
Anzahl der Vektoren einer Nebenklasse. Wieviele Vektoren hat eine Nebenklasse?
Nebenklassen sind immer abhängig von dem jeweiligen Untervektorraum  .
.
Grundsätzlich macht diese Frage nur sinn, wenn eine endliche Menge betrachtet wird. Irgendeine Anzahl an Elementen wird
betrachtet wird. Irgendeine Anzahl an Elementen wird  dann ja haben, wenn es endlich. Diese Zahl nennen wir einfach
dann ja haben, wenn es endlich. Diese Zahl nennen wir einfach 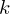 .
.
 selbst ist zu sich ist eine Nebenklasse, nämlich die Nebenklasse
selbst ist zu sich ist eine Nebenklasse, nämlich die Nebenklasse  .
.
Diese Nebenklasse hat die gleiche Anzahl an Element wie natürlich. Also genau
natürlich. Also genau  . (Nach dem Satz über die Anzahl von Elementen eins Vektoraumes)
. (Nach dem Satz über die Anzahl von Elementen eins Vektoraumes)
Wann könnte jetzt auf die Idee kommen, zu vermuten, dass auch jede äquivalente Nebenklasse gleichviele Elemente wie hat, und man könnte im ersten Versuch mal versuchen ein Bijektive Abbildung zwischen
hat, und man könnte im ersten Versuch mal versuchen ein Bijektive Abbildung zwischen  und
und  zu konstruieren. Klappt das, so ist klar, dass
zu konstruieren. Klappt das, so ist klar, dass  und
und  gleichmächtig sein müssen.
gleichmächtig sein müssen.
Das klappt mit . Denn die Surjektivitöt folgt aus der Definition der Nebenklasse und die Injetivität ist einfach mit
. Denn die Surjektivitöt folgt aus der Definition der Nebenklasse und die Injetivität ist einfach mit  .
.
 .
.Grundsätzlich macht diese Frage nur sinn, wenn eine endliche Menge
 betrachtet wird. Irgendeine Anzahl an Elementen wird
betrachtet wird. Irgendeine Anzahl an Elementen wird  dann ja haben, wenn es endlich. Diese Zahl nennen wir einfach
dann ja haben, wenn es endlich. Diese Zahl nennen wir einfach 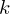 .
. selbst ist zu sich ist eine Nebenklasse, nämlich die Nebenklasse
selbst ist zu sich ist eine Nebenklasse, nämlich die Nebenklasse  .
.Diese Nebenklasse hat die gleiche Anzahl an Element wie
 natürlich. Also genau
natürlich. Also genau  . (Nach dem Satz über die Anzahl von Elementen eins Vektoraumes)
. (Nach dem Satz über die Anzahl von Elementen eins Vektoraumes)Wann könnte jetzt auf die Idee kommen, zu vermuten, dass auch jede äquivalente Nebenklasse gleichviele Elemente wie
 hat, und man könnte im ersten Versuch mal versuchen ein Bijektive Abbildung zwischen
hat, und man könnte im ersten Versuch mal versuchen ein Bijektive Abbildung zwischen  und
und  zu konstruieren. Klappt das, so ist klar, dass
zu konstruieren. Klappt das, so ist klar, dass  und
und  gleichmächtig sein müssen.
gleichmächtig sein müssen.Das klappt mit
 . Denn die Surjektivitöt folgt aus der Definition der Nebenklasse und die Injetivität ist einfach mit
. Denn die Surjektivitöt folgt aus der Definition der Nebenklasse und die Injetivität ist einfach mit  .
.
