Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
55
Orthogonale Reihententwicklung (Merkmale)
Entwicklung des Musters f(x) nach einem orthonormalen Funktionssystem.
Eine Menge von Vektoren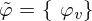 spannt einen Vektorraum V auf, wenn sich jedes Element aus V als Linearkombination von Vektoren aus
spannt einen Vektorraum V auf, wenn sich jedes Element aus V als Linearkombination von Vektoren aus 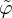 darstellen lässt. Die Koeffizienten c der Linearkombination sind die Entwicklungskoeffizienten.
darstellen lässt. Die Koeffizienten c der Linearkombination sind die Entwicklungskoeffizienten.
Wenn zu jedem Element aus V eindeutige Entwicklungskoeffizienten gehören, so bildet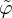
eine Basis für V .
Der Vektor f enthält die Abtastwerte des Musters.
Die Entwicklung eines Vektors f nach orthonormalen Basisvektoren aus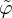 ergibt die eindeutigen Entwicklungskoeffizienten c wenn man die orthonormalen Basisvektoren
ergibt die eindeutigen Entwicklungskoeffizienten c wenn man die orthonormalen Basisvektoren 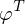 den Zeilen der Matrix
den Zeilen der Matrix 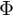 zuordnet. So kann man den Vektor c als Feature-Vektor verstehen, der das Muster eindeutig beschreibt.
zuordnet. So kann man den Vektor c als Feature-Vektor verstehen, der das Muster eindeutig beschreibt.

Die Vektoren f und c haben M und n Kompo-
nenten, M ≥ n, sodass die Matrix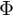 die Größe nM hat. n gibt dabei die Anzahl der verwendeten Basisvektoren an.
die Größe nM hat. n gibt dabei die Anzahl der verwendeten Basisvektoren an.
Dabei ist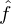 eine Approximation für f , und für n = M ist
eine Approximation für f , und für n = M ist 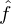 = f , wenn die Basisvektoren vollständig sind.
= f , wenn die Basisvektoren vollständig sind.
In der Praxis reduziert man die Anzahl der Basisvektoren auf die wichtigsten um die Informationen auf einen niedrigdimensionalen Feature-Vektor zu reduzieren. Dabei entsteht ein Fehler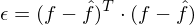 , der aufgrund des Orthogonalitätsprinzips minimal ist.
, der aufgrund des Orthogonalitätsprinzips minimal ist.
Die Entwicklungskoeffizienten c sind nichts anderes als die Beträge der Projektionen der einzelnen Werte aus f auf die Basisvektoren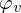 (siehe Orthogonalitätsprinzip).
(siehe Orthogonalitätsprinzip).
Eine Menge von Vektoren
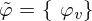 spannt einen Vektorraum V auf, wenn sich jedes Element aus V als Linearkombination von Vektoren aus
spannt einen Vektorraum V auf, wenn sich jedes Element aus V als Linearkombination von Vektoren aus 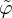 darstellen lässt. Die Koeffizienten c der Linearkombination sind die Entwicklungskoeffizienten.
darstellen lässt. Die Koeffizienten c der Linearkombination sind die Entwicklungskoeffizienten.Wenn zu jedem Element aus V eindeutige Entwicklungskoeffizienten gehören, so bildet
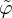
eine Basis für V .
Der Vektor f enthält die Abtastwerte des Musters.
Die Entwicklung eines Vektors f nach orthonormalen Basisvektoren aus
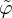 ergibt die eindeutigen Entwicklungskoeffizienten c wenn man die orthonormalen Basisvektoren
ergibt die eindeutigen Entwicklungskoeffizienten c wenn man die orthonormalen Basisvektoren 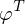 den Zeilen der Matrix
den Zeilen der Matrix 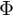 zuordnet. So kann man den Vektor c als Feature-Vektor verstehen, der das Muster eindeutig beschreibt.
zuordnet. So kann man den Vektor c als Feature-Vektor verstehen, der das Muster eindeutig beschreibt.
Die Vektoren f und c haben M und n Kompo-
nenten, M ≥ n, sodass die Matrix
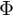 die Größe nM hat. n gibt dabei die Anzahl der verwendeten Basisvektoren an.
die Größe nM hat. n gibt dabei die Anzahl der verwendeten Basisvektoren an. Dabei ist
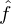 eine Approximation für f , und für n = M ist
eine Approximation für f , und für n = M ist 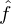 = f , wenn die Basisvektoren vollständig sind.
= f , wenn die Basisvektoren vollständig sind.In der Praxis reduziert man die Anzahl der Basisvektoren auf die wichtigsten um die Informationen auf einen niedrigdimensionalen Feature-Vektor zu reduzieren. Dabei entsteht ein Fehler
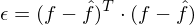 , der aufgrund des Orthogonalitätsprinzips minimal ist.
, der aufgrund des Orthogonalitätsprinzips minimal ist. Die Entwicklungskoeffizienten c sind nichts anderes als die Beträge der Projektionen der einzelnen Werte aus f auf die Basisvektoren
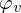 (siehe Orthogonalitätsprinzip).
(siehe Orthogonalitätsprinzip).Karteninfo:
Autor: JanBo
Oberthema: Digitale Bildverarbeitung
Thema: Mustererkennung
Schule / Uni: Universität Koblenz-Landau
Ort: Koblenz
Veröffentlicht: 13.09.2012

