This flashcard is just one of a free flashcard set. See all flashcards!
70
Was versteht man unter der Fourier-Transformation?

Man kann jede periodische, kontinuierliche Funktion als Summe von Sinus- und Kosinustermen konstruieren (siehe Bild rotes Signal).
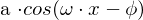
a = Amplitude
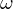 = Frequenz
= Frequenz = Phase
= PhaseDas Fourier-Integral beschreibt die ursprüngliche Funktion g(x) als Summe unendlich vieler Kosinus-/Sinusfunktionen mit kontinuierlichen (positiven) Frequenzwerten, wofür die Funktionen
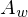 und
und 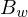 eindeutige Frequenzkoeffizienten liefern. Das Signal g(x) bzw, f(x) ist durch die zugehörigen Funktionen
eindeutige Frequenzkoeffizienten liefern. Das Signal g(x) bzw, f(x) ist durch die zugehörigen Funktionen 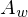 bzw.
bzw. 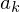 und
und 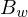 bzw.
bzw. 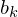 eindeutig definiert. Sie beschreiben die Amplitude und die Frequenz des Signals g(x) bzw. f(x).
eindeutig definiert. Sie beschreiben die Amplitude und die Frequenz des Signals g(x) bzw. f(x).Die Fourier-Transformation hat eine Reihe von Basisfunktionen (bestehend aus Sinus- und Cosinus-Funktionen) .. die sogenannten Fourier-Reihen.
Durch Kombination der Fourier-Reihen mit den eindeutigen Frequenzkoeffizienten wird das Signal g(x) bzw. f(x) im Ortsbereich eindeutig im Frequenzbereich G(w) bzw.
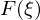 beschrieben.
beschrieben.Flashcard info:
Author: JanBo
Main topic: Digitale Bildverarbeitung
Topic: Mustererkennung
School / Univ.: Universität Koblenz-Landau
City: Koblenz
Published: 13.09.2012

