Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
21
Wie bestimmt man die momentane/lokale Änderungsrate einer Funktion f an einer Stelle x (mit der h-Methode)?
Man wählt zu einer Stelle 
eine „Nachbarstelle“ 
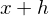und bildet mit den zugehörigen Funktionswerten 
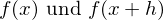den so genannten Differenzenquotienten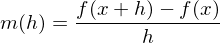 
Durch Ausklammern von h im Zähler und durch Kürzen mit h (bzw. geschicktes Umformen) wird der Bruch „reif für den Grenzübergang“: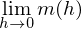
.
Nur wenn die Funktionsvariable (x) eine Zeit beschreibt, spricht man von momentaner Änderungsrate. In allen anderen Fällen sagt man lokale Änderungsrate.
Geometrisch entspricht dieser Grenzübergang dem Übergang von einer Sekante zur Tangenten.
Linktipp: Von der Sekanten zur Tangenten
eine „Nachbarstelle“ 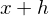und bildet mit den zugehörigen Funktionswerten 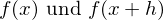den so genannten Differenzenquotienten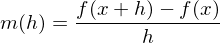 Durch Ausklammern von h im Zähler und durch Kürzen mit h (bzw. geschicktes Umformen) wird der Bruch „reif für den Grenzübergang“:
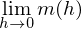.Nur wenn die Funktionsvariable (x) eine Zeit beschreibt, spricht man von momentaner Änderungsrate. In allen anderen Fällen sagt man lokale Änderungsrate.
Geometrisch entspricht dieser Grenzübergang dem Übergang von einer Sekante zur Tangenten.
Linktipp: Von der Sekanten zur Tangenten
Tags: Ableitung, Ableitungsfunktion, Änderungsrate, Begriffe, Differenzenquotient, h-Methode
Quelle:
Quelle:
Karteninfo:
Autor: www.mathematik-bw.de
Oberthema: Mathematik
Thema: 10. Klasse
Schule / Uni: Clara-Schumann-Gymnasium
Ort: Lahr
Veröffentlicht: 23.12.2009