Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!

Ein Problem ist, dass Punktkorrespondenzen oft nicht exakt sind. Die Fehler bei Punktkorrespondenzen können in zwei Klassen unterteilt werden:

• Schlechte Lokalisierung der Punktkorrespondenzen
• Falsche Korrespondenzen

Während in klassischen Schätzverfahren die Gesamtheit aller Messungen entsprechend dem kleinsten quadratischen Fehler berücksichtig wird, und dies im Falle von Ausreißern sehr
instabil ist, geht der RANSAC Algorithmus den umgekehrten weg.

1. Wähle m zufällige Mengen aus den Punktkorrespondenzen aus, wobei jede Menge aus 7 Korrespondenzen besteht, da die F-Matrix 7 unabhängige Parameter besitzt.

2. Für jede dieser Mengen wird 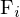berechnet.

3. Bestimme die Anzahl der Korrespondenzen, die mit 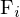konsistent sind. Ergebnis: 2 Mengen (konsistente und nicht-konsistente Korrespondenzen). Konsistent bedeutet, dass der Fehler beim Anwenden von  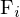 kleiner als ein bestimmter Schwellwert ist.

Beispiel einer Iteration
1. 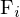wurde aus einer der Mengen bestimmt
2. wende nun 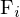auf alle Punktkorrespondenzen an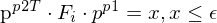

Durch die Epipolarbedingung wissen wir, dass bei einer korrekten F-Matrix mit korrekten Korrsepondenzen 0 herauskommen müsste ... in der Praxis nimmt man hier einen Schwellwert an.
Man behält letztendlich die Korrespondenzen, die mit einer 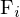die meisten Werte unterhalb des Schwellwertes erfüllen => größte konsistente Menge an Korrespondenzen


4. Behalte die größte konsistente Menge von Korrespondenzen.

5. Ende:
F ein letztes mal mit dem 8-Punkte-Algorithmus berechnen. Alle konsistenten Punktkorrespondenzen benutzen