This flashcard is just one of a free flashcard set. See all flashcards!
41
Wie ist die Kurzschreibweise für Modulo-Rechnen und welche Modulo-Gesetze gibt es?
Wir denieren 
 =
= 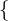 0, 1, ..., n - 1
0, 1, ..., n - 1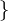 mit folgender Addition +
mit folgender Addition +
und Multiplikation
 . Seien k,
. Seien k, 
 Z
Z , dann gilt:
, dann gilt:
k +
 = (k +
= (k +  ) mod n
) mod n
k

 = (k
= (k 
 ) mod n
) mod n
(
 ,+
,+ ) und (
) und (
 ,
, 
 ) sind Monoide
) sind Monoide
(mit neutralen Elementen 0 bzw. 1)
Modulo-Gesetze
(a + b) mod n = ((a mod n) + (b mod n)) mod n
(a b) mod n = ((a mod n)
b) mod n = ((a mod n)  (b mod n)) mod n
(b mod n)) mod n
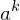 mod n =
mod n = 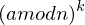 mod n
mod n

 =
= 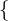 0, 1, ..., n - 1
0, 1, ..., n - 1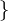 mit folgender Addition +
mit folgender Addition +
und Multiplikation

 . Seien k,
. Seien k, 
 Z
Z , dann gilt:
, dann gilt:k +

 = (k +
= (k +  ) mod n
) mod nk


 = (k
= (k 
 ) mod n
) mod n(

 ,+
,+ ) und (
) und (
 ,
, 
 ) sind Monoide
) sind Monoide(mit neutralen Elementen 0 bzw. 1)
Modulo-Gesetze
(a + b) mod n = ((a mod n) + (b mod n)) mod n
(a
 b) mod n = ((a mod n)
b) mod n = ((a mod n)  (b mod n)) mod n
(b mod n)) mod n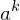 mod n =
mod n = 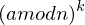 mod n
mod nTags: Algebraische Strukturen, VL 18.05.
Source:
Source:
Flashcard info:
Author: P-H-I-L
Main topic: Mathematik
Topic: Mathematische Strukturen
Published: 13.04.2010

