Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!

Originalbilder und ihre Repräsentation im Eigenspace (Feature-Vektor ).

Idee (Funktionsweise):

• Darstellung des Bildes als Spaltenvektor in dem das Bild Zeilenweise eingetragen wird
• Der Vergleich zwischen 2 Bildern und mit reduziert sich auf die Berechnung des Skalarproduktes . Je größer desto ähnlicher die beiden Bilder (Projektion des einen Vektor auf den anderen)
• Der Bildverktor ist zu groß für schnelle Berechnungen, daher reduziert man mittels einer linearen Transformation auf Featurevektor
• Für alle Eingabevektoren (Eingabebilder, z.B. rotierter Locher) bildet man den Mean-Vektor 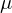. zieht ihn von jedem Bild ab und schreibtdie Bildvektoren in die Matrix
• Man bestimmt dann die Eigenvektoren von (z.B. mittels SVD)
• Man kann dann aus Linearkombination aus 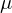und Eigenvektoren den Feature-Vektor im Eigenspace berechnen

Praktische Anwendung zur Objekterkennung:

• Für jede Klasse 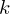werden  Feature-Vektoren im Eigenspace generiert (für jedes verwendete Bild unter verschiedenen Aufnahmebedingungen => Trainingsset) und entsprechend 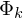(enthält verwendete Eigenvektoren aus K)
• die Vektoren einer Klasse 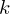bildern das Modell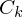
• die Korrelation zwischen zwei Bildern lässt sich dann approximiert durch die Eukldische Distanz aus berechnen
• ist wesentlich schneller, da wesentlich weniger Dimensionen hat

Klassifikation mittels Eigenspaces:
Die Klassifikation eines Bildvektors 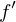(Voraussetzung: Bild befindet sich in Trainingsset) verläuft unter Verwendung des Modells 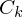und der Eigenwertmatrix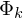
1. Transformation des Bildvektors 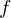in den Eigenspace =>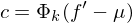
2. Vergleich mit allen Eigenspace-Vektoren aus
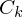
3. Wähle Vektor mit minimaler Distanz zu => Objekt gefunden!