Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
43
Finde eine Funktion deren Schaubild an der Stelle 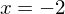 und die x-Achse durchschneidet, an der Stelle
und die x-Achse durchschneidet, an der Stelle 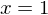 die x-Achse berührt und die y-Achse im Punkt (0/6) schneidet.
die x-Achse berührt und die y-Achse im Punkt (0/6) schneidet.
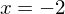 und die x-Achse durchschneidet, an der Stelle
und die x-Achse durchschneidet, an der Stelle 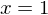 die x-Achse berührt und die y-Achse im Punkt (0/6) schneidet.
die x-Achse berührt und die y-Achse im Punkt (0/6) schneidet.Für die Lösung dieser Aufgabe benötigt man nicht unbedingt die Differenzialrechnung.
Die einfache Nullstelle liefert den Faktor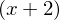 , die doppelte Nullstelle (bei x=1) entsprechend
, die doppelte Nullstelle (bei x=1) entsprechend 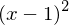 . Hieraus ergibt sich eine (Hilfs-)Funktion
. Hieraus ergibt sich eine (Hilfs-)Funktion 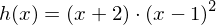 , die wir so in y-Richtung strecken, dass das Schaubild der gestreckten Funktion durch (0/6) verläuft.
, die wir so in y-Richtung strecken, dass das Schaubild der gestreckten Funktion durch (0/6) verläuft. 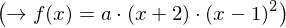
Aus (0/6) folgt: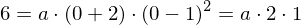
also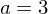 .
.
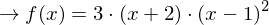
(Bei f(x) handelt es sich um eine ganzrationale Funktion, aber eine Darstellung in Summenform ist nicht gefordert! Kontrolliere das Ergebnis mit dem GTR/CAS.)
Die einfache Nullstelle liefert den Faktor
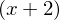 , die doppelte Nullstelle (bei x=1) entsprechend
, die doppelte Nullstelle (bei x=1) entsprechend 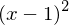 . Hieraus ergibt sich eine (Hilfs-)Funktion
. Hieraus ergibt sich eine (Hilfs-)Funktion 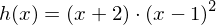 , die wir so in y-Richtung strecken, dass das Schaubild der gestreckten Funktion durch (0/6) verläuft.
, die wir so in y-Richtung strecken, dass das Schaubild der gestreckten Funktion durch (0/6) verläuft. 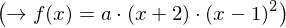
Aus (0/6) folgt:
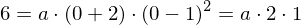
also
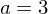 .
.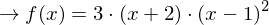
(Bei f(x) handelt es sich um eine ganzrationale Funktion, aber eine Darstellung in Summenform ist nicht gefordert! Kontrolliere das Ergebnis mit dem GTR/CAS.)
Tags: Funktion, ganzrational, Nullstelle, Produktform, Streckung
Quelle:
Quelle:
Karteninfo:
Autor: www.mathematik-bw.de
Oberthema: Mathematik
Thema: 10. Klasse
Schule / Uni: Clara-Schumann-Gymnasium
Ort: Lahr
Veröffentlicht: 23.12.2009

