This flashcard is just one of a free flashcard set. See all flashcards!
91
Beschreiben sie das Markov Modell
Wofür ist es geeignet, zu welchem Problem kann es dabei kommen und wie bekommt man dies unter Kontrolle?
Wofür ist es geeignet, zu welchem Problem kann es dabei kommen und wie bekommt man dies unter Kontrolle?
Das Markov Modell ist zur Modellierung von Sequenzen geeignet, d.h. es modelliert explizit die Abhängigkeit zwischen den Samples.
Die iid Anname wird zum Teil vernachlässigt.
Das Markov Modell besteht aus einer Menge der Zustände, den Anfangswahrscheinlichkeiten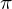 und den Übergangswahrscheinlichkeiten
und den Übergangswahrscheinlichkeiten  .
.
Die Übergangswahrscheinlichkeiten sind in der Übergangsmatrix A zusammengefasst.
Ein Problem für das Markov Modell ist die Tatsache das die Anzahl an Wahrscheinlichkeiten exponentiell mit der Satzlänge N steigt. Bei 1000 States (z.b. Wörter) und einer Satzlänger von N= 10 gibt es bereits 1000^10 Wahrscheinlichkeiten.
Durch das Einführen des Kontext kann man sich hier abhilfe schaffen. Dbaei werden nur Sequenzen bestimmter länger zusammen bewertet.
Die iid Anname wird zum Teil vernachlässigt.
Das Markov Modell besteht aus einer Menge der Zustände, den Anfangswahrscheinlichkeiten
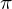 und den Übergangswahrscheinlichkeiten
und den Übergangswahrscheinlichkeiten  .
.Die Übergangswahrscheinlichkeiten sind in der Übergangsmatrix A zusammengefasst.
Ein Problem für das Markov Modell ist die Tatsache das die Anzahl an Wahrscheinlichkeiten exponentiell mit der Satzlänge N steigt. Bei 1000 States (z.b. Wörter) und einer Satzlänger von N= 10 gibt es bereits 1000^10 Wahrscheinlichkeiten.
Durch das Einführen des Kontext kann man sich hier abhilfe schaffen. Dbaei werden nur Sequenzen bestimmter länger zusammen bewertet.
Tags:
Source: CI Teil 2 Kapitel 6
Source: CI Teil 2 Kapitel 6
Flashcard info:
Author: Sepp Samuel
Main topic: Telematik
Topic: Computational Intelligence
School / Univ.: TU Graz
Published: 02.07.2014

