Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
17
H3: Den Abstand eines Punktes von einer Ebene berechnen.
Der Abstand d eines Punktes Q zur Ebene E (mit dem Punkt P und dem Normalvektor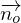 
(Länge = 1LE)) lässt sich am einfachsten mit der HNF (Hesse'sche Normalenform) berechnen.
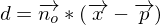
Beispiel: Welchen Abstand hat Q (5/3/1) zur
-Ebene?
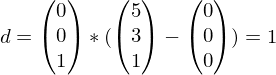
Hinweis: Auch andere Methoden, wie das Benutzen einer zu E senkrechten Geraden durch Q, um den zu Q nächsten Punkt in E zu finden, können benutzt werden.
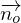(Länge = 1LE)) lässt sich am einfachsten mit der HNF (Hesse'sche Normalenform) berechnen.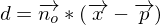Beispiel: Welchen Abstand hat Q (5/3/1) zur
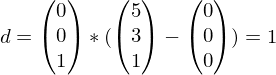
-Ebene?Hinweis: Auch andere Methoden, wie das Benutzen einer zu E senkrechten Geraden durch Q, um den zu Q nächsten Punkt in E zu finden, können benutzt werden.
Karteninfo:
Autor: Exinator
Oberthema: Mathematik
Thema: Abiturvorbereitung
Schule / Uni: MGS
Ort: Schwelm
Veröffentlicht: 28.03.2011