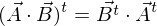Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
2
Die Verschiebung in einem Finiten Element 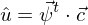 setzt sich zusammen aus den unnormierten Ansatzfunktionen
setzt sich zusammen aus den unnormierten Ansatzfunktionen 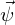 und den Koeffizienten
und den Koeffizienten 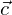 . Unter Verwendung der Normierungsmatrix
. Unter Verwendung der Normierungsmatrix 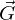 lassen sich die Knotenfreiwerte
lassen sich die Knotenfreiwerte 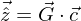 bestimmen. Leiten Sie damit die normierten Ansatzfunktionen
bestimmen. Leiten Sie damit die normierten Ansatzfunktionen 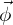 her, so dass gilt:
her, so dass gilt: 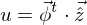 .
.
Formulieren Sie die Steifigkeitsmatrix für ein Balkenelement
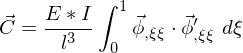
unter Verwendung der unnormierten Ansatzfunktion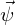 .
.
Hinweis: Für die Transponierung eines Matrizenproduktes gilt allgemein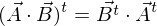
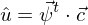 setzt sich zusammen aus den unnormierten Ansatzfunktionen
setzt sich zusammen aus den unnormierten Ansatzfunktionen 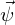 und den Koeffizienten
und den Koeffizienten 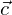 . Unter Verwendung der Normierungsmatrix
. Unter Verwendung der Normierungsmatrix 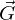 lassen sich die Knotenfreiwerte
lassen sich die Knotenfreiwerte 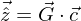 bestimmen. Leiten Sie damit die normierten Ansatzfunktionen
bestimmen. Leiten Sie damit die normierten Ansatzfunktionen 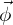 her, so dass gilt:
her, so dass gilt: 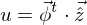 .
.Formulieren Sie die Steifigkeitsmatrix für ein Balkenelement
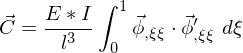
unter Verwendung der unnormierten Ansatzfunktion
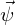 .
.Hinweis: Für die Transponierung eines Matrizenproduktes gilt allgemein