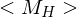Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
36
Beweis: spezielles Halteproblem ist nicht rekursiv
Zum Zwecke des Widerspruchs nehmen wir an, dass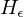 
entscheidbar ist. Es gibt also eine TM 
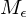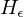, die entscheidet.
Konstruieren nun eine TM
, die 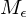als Unterprogramm aufruft und das Halteproblem entscheidet. (Da H nicht entscheidbar ist, kann 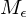also nicht ex.)
Die TM arbeiten wie folgt:
1.) Falls die Eingabe keine korrekte GN ist, verwirft die Eingabe
2.) sonst, auf alle Eingaben der Form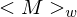
berechnet die GN einer TM 
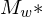mit folgenden Eigenschaften:
- falls die TM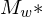 auf leere Eingabe startet, schreibe w aufs Band und simuliere M auf w.
- auf anderen Eingaben, verhält sie sich beliebig
3.) schreibt GN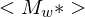 
aufs Band und startet 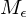auf dieser Eingabe und übernimmt deren Akzeptanzverhalten.
Korrektheit:
1.Fall: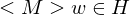
=> M hält auf w => 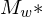hält auf 
, da sonst M auf w nicht simuliert worden wäre =>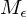 
akzepti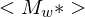ert => akzeptiert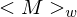
2. Fall: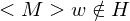
=> M hält nicht auf w => 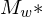hält nicht auf 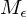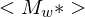=> verwirft => verwirft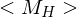 
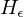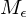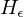entscheidbar ist. Es gibt also eine TM , die entscheidet.Konstruieren nun eine TM
, die 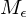als Unterprogramm aufruft und das Halteproblem entscheidet. (Da H nicht entscheidbar ist, kann 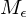also nicht ex.)Die TM
arbeiten wie folgt:1.) Falls die Eingabe keine korrekte GN ist, verwirft
die Eingabe2.) sonst, auf alle Eingaben der Form
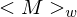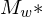berechnet die GN einer TM mit folgenden Eigenschaften:- falls die TM
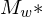auf leere Eingabe startet, schreibe w aufs Band und simuliere M auf w.- auf anderen Eingaben, verhält sie sich beliebig
3.)
schreibt GN 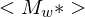aufs Band und startet 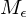auf dieser Eingabe und übernimmt deren Akzeptanzverhalten.Korrektheit:
1.Fall:
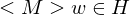=> M hält auf w => 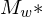hält auf , da sonst M auf w nicht simuliert worden wäre => 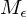akzepti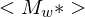ert => akzeptiert 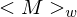2. Fall:
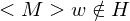=> M hält nicht auf w => 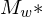hält nicht auf 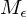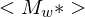=> verwirft => verwirft 