This flashcard is just one of a free flashcard set. See all flashcards!
31
Wie löst man das folgende Tangentenproblem (Typ 2):
Eine Tangentensteigung ist gegeben. Gesucht ist/sind die Tangente(n) an das Schaubild mit dieser Steigung.
Eine Tangentensteigung ist gegeben. Gesucht ist/sind die Tangente(n) an das Schaubild mit dieser Steigung.
Leite die Funktion zum Schaubild ab und setzte die Ableitungsfunktion mit der gegebenen Steigung gleich. Die Gleichung besitzt eine oder mehrere Lösungen, je nachdem, ob es eine oder mehrere Tangenten mit der geforderten Steigung gibt.
Jede Lösung entspricht dem x-Wert eines Berührpunktes. Den zugehörigen y-Wert erhält man durch Einsetzen des x-Wertes in f(x).
Durch Verschiebung der Ursprungsgeraden mit der geforderten Steigung in x- und y-Richtung erhalten wir die Tangentengleichung:
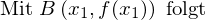
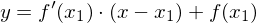
Bemerkungen:
Beim Schaubild der Kehrwertfunktion gibt es für alle Steigungen außer m=0 zwei Tangenten.
Bei Parabeln gerader Ordnung gibt es zu jeder Steigung genau eine Lösung.
Bei ganzrationalen Funktionen mit einem Grad > 2 kann es mehrere Lösungen geben.
Jede Lösung entspricht dem x-Wert eines Berührpunktes. Den zugehörigen y-Wert erhält man durch Einsetzen des x-Wertes in f(x).
Durch Verschiebung der Ursprungsgeraden mit der geforderten Steigung in x- und y-Richtung erhalten wir die Tangentengleichung:
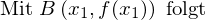
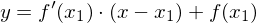
Bemerkungen:
Beim Schaubild der Kehrwertfunktion gibt es für alle Steigungen außer m=0 zwei Tangenten.
Bei Parabeln gerader Ordnung gibt es zu jeder Steigung genau eine Lösung.
Bei ganzrationalen Funktionen mit einem Grad > 2 kann es mehrere Lösungen geben.
Tags: ganzrational, Tangente, Verschiebung
Source:
Source:
Flashcard info:
Author: www.mathematik-bw.de
Main topic: Mathematik
Topic: 10. Klasse
School / Univ.: Clara-Schumann-Gymnasium
City: Lahr
Published: 23.12.2009

