Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
49
Transitive Hülle und kanonische Überdeckung von FDs
Gegeben sei eine Menge F von FDs.
Die Menge aller aus F logisch ableitbaren FDs wird als transitive Hülle F+ bezeichnet. Die Armstrong-Regeln bilden einen korrekten und vollständigen Ableitungskalkül für die FDs in F+.
Die kanonische Überdeckung ist intuitiv die kleinste noch äquivalente Menge von FDs. Diese wird durch vier Schritte aus einer Menge F von FDs der Form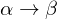 hergeleitet:
hergeleitet:
Die Menge aller aus F logisch ableitbaren FDs wird als transitive Hülle F+ bezeichnet. Die Armstrong-Regeln bilden einen korrekten und vollständigen Ableitungskalkül für die FDs in F+.
Die kanonische Überdeckung ist intuitiv die kleinste noch äquivalente Menge von FDs. Diese wird durch vier Schritte aus einer Menge F von FDs der Form
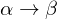 hergeleitet:
hergeleitet:- Linksreduktion: Für alle
 überprüfen, ob
überprüfen, ob  überflüssig ist (mit Hilfe der AttrHülle). Wenn ja, dann
überflüssig ist (mit Hilfe der AttrHülle). Wenn ja, dann  aus
aus  nehmen.
nehmen. - Rechtsreduktion: Für alle
 prüfen, ob
prüfen, ob  überflüssig ist, ggf.
überflüssig ist, ggf.  aus
aus  nehmen.
nehmen. - Alle leeren FDs der Form
 entfernen.
entfernen. - Mit Hilfe der Vereinigungsregel alle
 , ...
, ... 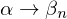 zusammenfassen
zusammenfassen
Tags:
Quelle: Kapitel 6, Folien 12-16
Quelle: Kapitel 6, Folien 12-16
Karteninfo:
Autor: kread
Oberthema: Informatik
Thema: Datenbanken
Schule / Uni: Universität Koblenz-Landau
Ort: Koblenz
Veröffentlicht: 18.10.2010

