Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
96
Explain the Singular Value Decomposition!
Given 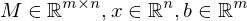 , a system
, a system
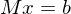
might be over- or under-determined. We still want to compute an approximate solution.
For any such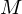 , there exists the Singular Value Decomposition
, there exists the Singular Value Decomposition
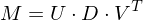 where
where
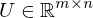 is orthonormal:
is orthonormal: 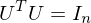
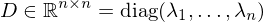
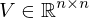 is orthonormal:
is orthonormal: 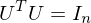
From this, we can construct the pseudo-inverse
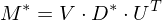
where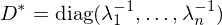
where
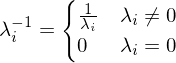
Due to numerical imprecisions, we use
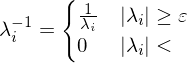
Now, we can compute a solution:
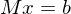
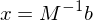
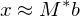
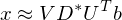
This solution is
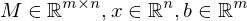 , a system
, a system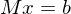
might be over- or under-determined. We still want to compute an approximate solution.
For any such
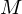 , there exists the Singular Value Decomposition
, there exists the Singular Value Decomposition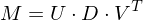 where
where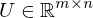 is orthonormal:
is orthonormal: 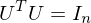
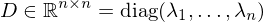
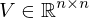 is orthonormal:
is orthonormal: 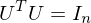
From this, we can construct the pseudo-inverse
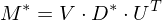
where
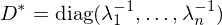
where
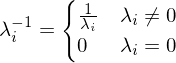
Due to numerical imprecisions, we use
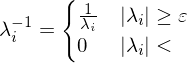
Now, we can compute a solution:
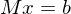
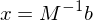
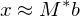
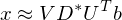
This solution is
- a solution in the least-squares sense if M is overdetermined
- a solution in the last-norm sense if M in underdetermined
Karteninfo:
Autor: janisborn
Oberthema: Informatik
Thema: Computergrafik
Schule / Uni: RWTH Aachen
Ort: Aachen
Veröffentlicht: 18.05.2022

