Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!

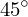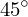Algorithm idea: Voronoi diagram is equivalent to the highest points of a set of cones centered on the sites. By sweeping a inclined plane through the set of cones, all points where at least 3 cones intersect (i.e., the Voronoi vertices) are enumerated.

The algorithm maintains:

• List of all currently active arc segments, each associated with one site
• An event priority queue, containing the positions of the next upcoming site events and circle events

Site event
Occurs when the sweep line crosses a site. This causes a new arc (of initially zero width) to be inserted at the position of the site. Find into which arc segment the new site falls. Split the arc segment. Insert new arc segment in between. Now, generate upcoming circle events: Consider the neighboring arc triples containing the new arc. If these triples have distinct sites, create a new circle event by computing the circumcircle of the three sites and insert a circle event at the outermost edge of the circumcircle (but only if this point lies still before the sweep line).

If the arc which was split by the insertion had a pending circle event, this circle event is removed and new circle events are computed based on the new neighborhood of the affected arcs.

Circle event
When the sweep line leaves the circumcircle of three sites the inclined halfplane passes a point that is equidistant to the three sites. At this time, the center arc of the three sites shrinks to zero. Thus, the arc is removed from the arc list and a new Voronoi vertex is created.

Generating a Delaunay triangulation
At every circle event, three sites lie on an empty circumcircle. By connecting the three sites, we obtain a triangle with the Delaunay property.