Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
4
How many neighbors does each Voronoi cell have in a planar Voronoi diagram, on average?
In 2D, the Voronoi diagram is dual to the Delaunay triangulation. For each triangle mesh, we know that
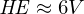
i.e., each vertex is adjacent to 6 other vertices, on average. Since vertices in the Delaunay triangulation are dual to Voronoi cells, each Voronoi cell has 6 neighboring cells, on average.
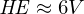
i.e., each vertex is adjacent to 6 other vertices, on average. Since vertices in the Delaunay triangulation are dual to Voronoi cells, each Voronoi cell has 6 neighboring cells, on average.
Karteninfo:
Autor: janisborn
Oberthema: Informatik
Thema: Computergrafik
Schule / Uni: RWTH Aachen
Ort: Aachen
Veröffentlicht: 18.05.2022

